Funckja liniowa fawww: Witam, przychodzę do was z pewnym zadaniem z którego mogę dostać pozytywną ocene, a sam raczej nie jestem w stanie jego rozwiązać..:( Dlatego zwracam się do was drodzy matematycy z prośbą o rozwiązanie i krótkie wyjaśnienie . Z góry dziękuje Sporząd wykres funkcji y = f(x) oraz dla m∊R określ liczbę rozwiązań równania f(x) = m, gdy: a) f(x) = |x+1|+x b) f(x)= √x₂ =4x +4 −|x+1| c) f(x)= √x₂ −6x +9 + √x₂

Anna: Pomogę Ci, a tymczasem napisz, czy w b) ma być √x²+4x+4 ?

fawww: tak, przepraszam pomyliłem się i tak samo w c powinno być √x²−6x+8 + √x², dziękuje

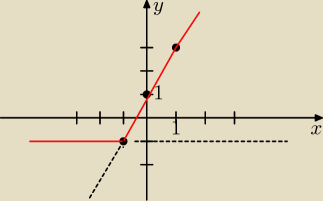
Anna: a) f(x) = Ix+1I + x 1⁰. x+1≥0, x≥−1 2⁰ x+1<0, x<−1 f(x)=x+1+x = 2x+1 f(x) = −(x+1)+x = −x−1+x = −1 Wykres na rysunku. Ilość rozwiązań równania f(x)=m : 0 rozwiązań dla m∊(−∞,−1) 1 rozwiązanie dla m∊ (−1,∞) nieskończona ilość rozwiązań dla m= −1.

fawww: a czy była by pani tak uprzejma i zapisała mi to jeszcze we wzorze wartości bezwględnej? Mniej

	⎧	2x−2 gdy x<2
więcej aby to wyglądało następująco : f(x)=	⎩	x+3 gdy x=5	wartości w klamrze

oczywiście zmyśliłem przepraszam, że panią wykorzystuje

fawww: oczywiście chodzi mi o zapisanie tych 2 półprostych

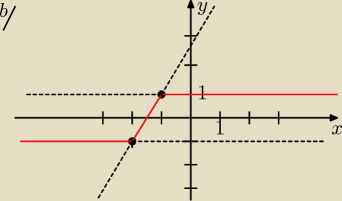
Anna: b) f(x)=√x²+4x+4 − Ix+1I = √(x+2)² −Ix+1I = Ix+2I − Ix+1I Wyznaczamy miejsca zerowe z obu wartości bezwzględnych: x+2=0 ⇒ x= −2, x+1=0 ⇒ x= −1 Oś dzielimy na przedziały : 1⁰ x∊(−∞,−2) Wtedy: f(x)=−(x+2)+(x+1) = −x−2+x+1 = −1 2⁰ x∊<−2,−1) Wtedy: f(x)=x+2+x+1 = 2x+3 3⁰ x∊<−1,∞) Wtedy: f(x)=x+2−(x+1) = x+2−x−1= 1 Na podst. wykresu ilość rozwiązań równania f(x)=m jest równa: 0 rozwiązań dla m ∊(−∞,−1) U(1,∞) 1 rozwiązanie dla m ∊(−1, 1) nieskończona ilość rozwiązań dla m= −1 oraz dla m =1.

Anna: W punkcie a) równania półprostych masz wyznaczone w każdym podpunkcie, tzn. f(x) = 2x+1 dla x≥ −1 f(x) = −1 dla x< −1 O to Ci chodziło?

fawww:

	⎧	2x+1 gdy x≥1
Tak, chyba o to Czyli będzie f(x)=	⎩	−1 gdy x< −1	Dziękuje

Anna: W punkcie b) podobnie: f(x) = −1 dla x∊(−∞, −2) f(x) = 2x+3 dla x∊<−2,−1) f(x) = 1 dla x∊<−1,∞)

Anna: c) Podobnie. Spróbuj. f(x) = √(x−3)² + √x² = Ix−3I + IxI

fawww: to spróbuje ogarnąć a i b I spróbuje c) Dziękuje

fawww: Tylko nie wiem za bardzo jak pani podzieliła f(x) = Ix+1I + x na x+1≥0, x≥−1 i x+1<0, x<−1

fawww: i nie pojmuje o co chodzi z tym m

Anna: Zasada jest taka, że każdą wartość bezwzględną, na podstawie jej definicji, rozważa się w 2 przypadkach: x dla x≥0 IxI = −x dla x <0

fawww: Dobrze tylko skąd się wzięło x≥−1 i x<−1

Anna: Z m to jest tak (wytłumaczę Ci w taki sposób, żebyś miał szansę pojąć). Patrząc na wykonany wykres wyobraź sobie poziome, równoległe do siebie proste, które przecinają cały układ współrzędnych. Jedne z nich przetną nasz wykres w jednym punkcie (wtedy mówimy, że jest jedno rozwiązanie), inne przetną go w 2 punktach (wtedy są 2 rozwiązania − takich u Ciebie nie było), albo proste te w ogóle nie "spotkają" się z danym wykresem (wtedy nie ma rozwiązań). Te proste poziome mają równania : y = m, Czy to Ci coś rozjaśnia?

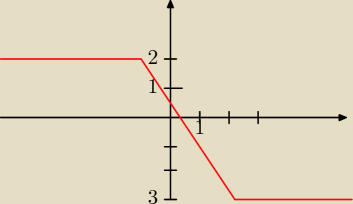
fawww: a i w podręczniku b jest inaczej:

Anna: Ponieważ rozwiązaniem nierówności x+1 ≥ 0 jest x≥ −1, a dla x+1<0 jest x < −1.

Anna: Ten rysunek, to do punktu c?

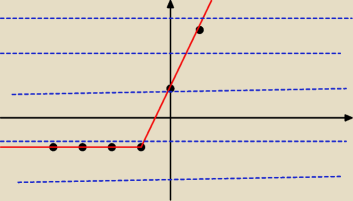
fawww: tą niebieską linią zaznaczyłem m.. Chyba pojąłem o co chodzi już mi się rozjaśniło z tym y=m dziękuje

Anna: Co Ci się nie zgadza z podręcznikiem? Na pewno musi być tak, jak napisałam. .

fawww: ten rysunek to do punktu B pani Anno Musiałą pani popełnić jakiś błąd.. f(x)= |x−2| − |x=1|

	⎧	3 gdy x∊(−∞; −1)
f(x) =	⎨	−2x+1 gdy x∊<−1;2)
	⎩	−3 gdy x∊2;+∞)

Anna: ok. Powodzenia!

fawww: haha! dziękuje bardzo mi pani pomogła zaraz spóbuje sam rozwiązać b i c

Anna: Do punktu b) zrobiłam wg wzoru, jaki podałeś na początku. Twój wzór funkcji w ostatnim zapisie pochodzi z innego wzoru. Musiałoby być: f(x)= √x²−4x+4 + ?

fawww: nie no √(x−2)² = |x−2|

fawww: my podobne zadanie do podpunktu b robiliśmy w zeszycie jak zrobię dobrze to wszystko napiszę o ile nie zasne

Anna: Ale na początku podałeś √x²+4x+4.

Anna: Dobrze, to ja zobaczę już jutro, bo teraz muszę skończyć.

fawww: dobrze to ja również jutro wstawię postaram się nie zapomnieć i chociaż w ten sposób się pani odwdzięczyć Dobranoc

fawww: b mi wyszło jeszcze tylko c uff

fawww: i c też wyszło! jutro pani wszystko przepisze ew. zeskanuje pozdrawiam i jeszcze raz bardzo dziękuje rozjaśniła mi pani wszystko Zaczne wchodzić tutaj częściej gdyby pani mogła to bym prosił o kontakt na gg 5441227 Jeśli się pani odezwie to będę pani wysyłał linki do moich zadań domowych ponieważ jest pani genialnym tłumaczem! Może pani pracować w szkole

Anna: Cieszę się, fawww, że udało Ci się uzyskać dobre wyniki. Gratuluję! To trzeba raz dobrze zrozumieć, zapamiętać i nigdy nie będziesz miał kłopotu z wartością bezwzględną. Przykro mi, ale w punkcie b) rzeczywiście wkradł mi się błąd znakowy. Zdarzyć może się każdemu, jak widać. Cieszę się, że udało Ci się to naprawić samemu. Miło mi,że pomogłam Ci w zrozumieniu tego tematu. Dzięki za miłe słowa. W szkole to ja już się napracowałam, a teraz na zasłużonej emeryturze pomagam, komu tylko jest okazja. Chętnie i Tobie pomogę np. tu na forum. Jesteś w kl. II − domyślam się.Gg niestety nie mam. Pozdrawiam Cię i życzę powodzenia.

fawww: Jestem w kl.1 LO Mat−fiz Jeszcze raz dziękuje

Anna: Dopiero w I LO ! To jeszcze do matury trochę Ci zostało czasu i pracy. Z jakiego podręcznika korzystacie? A zadanie dzisiejsze o funkcji przemyślałeś? Ciekawe. Skąd je miałeś?