ekstrema funkcji justynka91: wyznaczyć wszystkie ekstrema funkcji y=xlnx

Godzio: f(x) = x * lnx f'(x) = lnx + 1

	1
f'(x) = 0 ⇒ lnx = −1 ⇒ x =
	e

	1		1
f(		) = −		−− minimum
	e		e

justynka91: no, tak, tak... a skąd wiemy, ze to minimum

Godzio: Bo pochodna zmienia tam znak z minusa na + (wystarczy narysować wykres pochodnej)

justynka91: acha, no spoko... Mam jeszcze taki jeden przykład, który nie daje mi spokoju y=x−√2x Obliczyłam, minimum wyszło 1/4 Problem jest z obliczeniem wartości tego x... ( w pkt X=1/4 funkcja przyjmuje minimum lokalne równe −49/4) No i właśnie nie wiem jakim cudem wyszło to −49/4

Godzio: Ja też

Godzio: Przepisz najpierw porządnie przykład

justynka91: y=x−√x

justynka91: Pewnie jakiś wzór skróconego mnożenia, no nie wiem...

Godzio: D = <0,∞) f(x) = x − √x

	1		1
f'(x) = 1 −		= 0 ⇒ 2√x = 1 ⇒ x =
	2√x		4

	1		1		1		1		2		1
f(		) =		−		=		−		= −
	4		4		2		4		4		4

	1		1
(		,−		)
	4		4

justynka91: Może w odp jest błąd...

justynka91: a coś takiego... polecenie to samo... pytanie o ekstrema.. y= (x+3)³/(x+1)²

Godzio: D = R − {−1}

	3(x + 3)2(x + 1)2 − 2(x + 3)3(x + 1)
f'(x) =		=
	(x + 1)4

	(x + 3)2(x + 1)(3(x + 1) − 2(x + 3))		(x + 3)2(x − 3)
=		=
	(x + 1)2		(x + 1)3

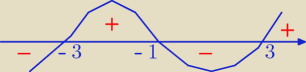
f'(x) = 0 ⇒ x = −3 lub x = 3

(x + 3)2(x − 3)
	> 0
(x + 1)3

(x + 3)³(x − 3)(x + 1) > 0 f(−3) = 0 − minimum lokalne

	63		33 * 23		27
f(3) =		=		=		− minimum lokalne
	42		24		2

justynka91: Jejku... Jak Wy to szybko rozw Dziękuje, jak zwykle machnęłam się w obliczeniach.

angela: mam pytanie odnośnie tego jak rysowałaś ten wykres ... rysowanie wykresu zaczęła od prawej strony? Czyli : 1. patrzysz na wartość przy najwyższym stopniu wielomianu. 2. rysujesz od prawej str (jeśli wartość jest + to rysujesz od góry; jeśli jest − to od dołu). Dobrze to rozumiem