Pochodne Godzio: No to podam przykład funkcji złożonej, z której policzę pochodną, a Ty spróbujesz z paroma innymi przykładami: f(x) = √tg(ln(x³)) Pochodna funkcji złożonej to nic innego jak iloczyn pochodnych poszczególnych funkcji

	1
(√ )' =
	2√

	1
(tg( ))' =
	cos2( )

	1
(ln( ))' =
	( )

(xⁿ) = nx^{n − 1} Korzystając z tego od razu liczę pochodną zaczynając od zewnątrz (można od wewnątrz, ale mi tak wygodnie)

	1		1		1
f'(x) =		*		*		* 3x2
	2√tg(ln(x3))		cos2(ln(x3)		x3

	3
f'(x) =
	2x√tg(ln(x3))cos2(ln(x3))

Postępując podobnie policz takie cuda: a) f(x) = √ln(x⁴) b) g(x) = e^cos2√x2

	1
c) h(x) = ln(sin(		))
	x2

I na sprawdzenie czy znasz wzory na pochodną iloczynu i ilorazu (jak nie znasz to powiedz, przećwiczymy)

	ex
a) i(x) =
	x + 1

	cosx + sinx
b) j(x) =
	√x

c) k(x) = cos²x * e^x d) m(x) = ln(x²) * ⁵√x³

Eta: 1/ oblicz pochodną y= log_xa

Godzio: Kejt ostatnią tą pochodną komuś robiła nawet

Kejt: tak..zastanawiam się tylko czy dobrze tak czy siak.. do tej pory jestem z siebie dumna

Godzio:

	1		1   −   xlna		1
(logxa)' = (		)' =		= −
	logax		loga2x		xln(a)loga2x

Godzio: Idę się pouczyć niemieckiego trochę, wrócę za 30 min i zobaczę co Ty tu wymodziłaś

Kejt: a) f(x) = √ ln (x⁴)

	1		1		4x3
f'(x) =		*		* 4x3 =		=
	2√ ln (x4)		x4		2x4√ ln (x4)

	2
	x√ ln (x4)

tak?

Eta: Można też tak

	lna
logxa=
	lnx

	lna
y' = −
	x*ln2x

TOmek: wybaczcie, ze spamuje ale mam pytanko do Godzia, czy Twoja nauka opierała sie tylko na szkoła/sam w domu, czy były jakies korki u nauczycieli?

Godzio: Ketj TOmek żadnych korków, moim zdaniem to niepotrzebne wyrzucanie pieniędzy jak można samemu się nauczyć, wystarczą chęci A zadania robiłem z kolegą, co prawda bardziej ja go uczyłem, ale czasami to on mi coś pomagał

TOmek: dzieki, juz nie przeszkadzam

Kejt: z tym cos²√x² da się coś przedtem zrobić, czy nie ruszać?

Kejt:

	1
c) h(x) = ln(sin(		))
	x2

	1		1		1
h'(x) =		* cos(		) * (−		) =
	1   sin( )   x2		x2		x4

	1   1   cos( ) * (− )   x2   x4
	1   sin( )   x2

i chyba tyle..? czy na tg zamienić?

Godzio: W sumie bez sensu trochę napisałem Popraw sobie cos²³√x² Ale lepiej tego nie ruszać

Godzio:

	1
Ewentualnie na ctg, (		)' = ? −− jeszcze raz ile to jest ?
	x2

Kejt: fakt.. ctg według wzoru:

	a		a
(		)' = −
	x		x2

	1		1
(		)' = −
	x2		x4

czy coś pokręciłam?

Godzio:

	a
A wzór jest taki dlatego, że (		)' = a * (x−1)' = a * −1 * x−2
	x

Ogólnie to tyczy się (x^α)' = α * x^{α − 1} dla α ∊ R

Kejt: czyli dobrze..?

Godzio: Nie

	1		2
(		)' = (x−2)' = −2 * x−2 − 1 = −2 * x−3 = −
	x2		x3

Kejt: ach.. wstrętna dwójka.. przypomniało mi się "Ja bym pozabijał na korkach jakby mi ktoś takie błędy robił" mam nadzieję, że jeszcze wytrzymujesz..

Godzio: Jestem tak wykończony, że nie mam sił się wkurzać, dzisiaj 6 h siedziałem z niemieckim, a zrobiłem tylko gramatykę ... A matura już w środę

duu duu: Przepraszam że się wepchnę, ale jak przekształcić funkcję f(x)= cox + ¹₂ ?

kylo: godzio... ty jestes w maturalnej? kurde, ja niby w II lo, z matmy nie kuleje, wrecz przeciwnie ale nic a nic poza material nie wychodze bo mi sie nie chce. A tutaj to naprawde widze sa checi, zapal i motywacja. Pelen podziw z mojej strony.

Godzio: Tak kylo byłem w maturalnej bo szkoła się już skończyła duu duu

	1		π		π   x +   3		π   x −   3
f(x) = cosx +		= cosx + cos(		) = 2cos		cos		=
	2		3		2		2

	3x + π		3x − π
= 2cos		cos
	6		6

Na przykład tak,

duu duu: ale mi chodzi na funkcji, graficznie

Kejt: b) g(x) = e^{cos2 3√x2} pozwolisz, że będę teraz na samej potędze liczyła..bo małe literki są..

	1
−sin 3√x2 *		* 2x
	3√x2

tego 2x nie jestem pewna.. ale już zostawię..

	1		−sin 3√x2 2x
−sin 3√x2 *		* 2x =
	3√x2		3√x2

Godzio: To na szczęście nie mieści się na potędze

	2
Policzę najpierw: (cos23√x2)' = cos2x2/3 = 2cos3√x2 * sin3√x2 *		x−1/3 =
	3

	4cos3√x2 * sin3√x2		2sin23√x2
=		=
	33√x		33√x

Pochodna całości to po prostu:

	2sin23√x2
(ecos23√x2)' = ecos23√x2 *
	33√x

Jak masz e^..... to pochodna z tego to: e^..... * (.....)'

Kejt: dobra..ale to się trochę nie zgadza z tym moim.. znów coś zepsułam

Godzio: Zauważ że pierwszą funkcją jest potęga (cos(x))² = pochodna ² * pochodna cosinusa = 2 * cosx * (−sinx) Ja tam minusa nie uwzględniłem przy pochodnej cosinusa ...

Kejt: ech.. 1:2 dla pochodnych..

Kejt: a te wzory to niby znam.. tzn. to moje "znanie" wygląda w ten sposób, że je sobie wydrukowałam i leżą teraz przede mną na biurku

Godzio: No to lecimy: (f * g)' = f' * g + f * g'

	f		f' * g − f * g'
(		)' =
	g		g2

W praktyce:

	3
(4√x3 * lnx)' = (x(3/4))' * lnx + 4√x3 * (lnx)' =		* x−1/4 * lnx + 4√x3 *
	4

	1
		=
	x

3lnx		1		3lnx + 4
	+		=
44√x		4√x		4√x

	ex + lnx		(ex + lnx)' * sinx − (ex + lnx) * (sinx)'
(		)' =		=
	sinx		sin2x

	1   (ex + )*sinx − (ex + lnx) * cosx   x
=		No i tam można bawić się w upraszczanie
	sin2x

... Chcesz więcej przykładów ?

Kejt:

	ex
a) i(x) =
	x+1

	ex(x+1) − ex		ex(x+1 −1)		ex * x
i'(x) =		=		=
	x2+2x+1		x2+2x+1		x2+2x+1

(x+1)' = 1 + 0 = 1 więc już tego nie pisałam.. tak?

Godzio: Git

Kejt:

	cosx + sinx
b) j(x) =
	√x

	(cosx + sinx)' * √x − (√x)' * (cosx + sinx)
j'(x) =		=
	x

1   √x(cos x − sin x) − (cosx + sinx)   2√x
x

Godzio: √x² = x ? a nie |x| ?

Godzio: Ale w sumie przy tym zapisie to tak może być

Kejt: no właśnie się zastanawiałam.. ale mam tak w przykładach na stronce: https://matematykaszkolna.pl/strona/359.html (drugie od dołu) i tam tego nie uwzględniono..

Godzio: No zgadzam, się w tym wyrażeniu mam √x także nie trzeba zapisać bezwzględności

Kejt: c) k(x) = cos²x * e^x k'(x) = (cos²x)' * e^x + cos²x * e^x = i teraz moje pytanie brzmi.. mam to tak dalej zrobić z tym cos²x jak Ty w poście z 23:30?

Godzio: Tak

Kejt: k'(x) = (cos²x)' * e^x + cos²x * e^x = 2 * cosx * (−sinx) * e^x + cos²x * e^x = cosx * e^x (−2sinx + cosx)

Godzio: Jeśli chciałbyś to ładniej zapisać to może tak: −2sinxcosxe^x + cos²xe^x = −e^x(sin2x − cos²x)

Kejt: "chciałbyś" dziękuję Godziu.. tak wiem, to literówka..

Kejt: d) m(x) = ln(x²) * ⁵√x³

	1		1
m'(x) =		* 2x * 5√x3 + ln(x2) *		* 3x2 =
	x2		25√x3

2x5√x3		ln(x2) * 3x2		25√x3		ln(x2) * 3x2
	+		=		+
x2		25√x3		x		25√x3

Godzio: Dobra to skoro już to opanowałaś, to przejdziemy nieco dalej. Pochodna przydaje się do różnych rzeczy, między innymi do wyznaczenia ekstremum (maksimum i minimum) monotoniczności funkcji, wypukłości i wklęsłości. Weźmy taką funkcję: f(x) = xe^x Teraz chcemy określi gdzie funkcja rośnie i maleje, oraz określić jej przedziały monotoniczności w tym celu liczymy pierwszą pochodną: f'(x) = e^x + xe^x Gdy f'(x) > 0 −− to funkcja jest rosnąca, gdy f'(x) < 0 to funkcja jest malejąca, jeśli f'(x) = 0 to osiąga maksimum lub minimum. Trzeba pamiętać że te ekstrema są rzeczywiście ekstremami gdy pochodna w tych punktach zmienia znak, tzn. 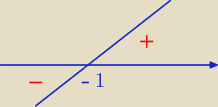rysujesz sobie przybliżony wykres pochodnej i sprawdzasz czy zmienia znak (dokładnie tak jak równania wielomianowe) Więc sprawdzamy: f'(x) > 0 e^x(1 + x) > 0 /:e^x bo e^x > 0 1 + x > 0 x > −1 f(x) ↗ ⇔ x ∊ (−1,∞) f(x) ↘ ⇔ x ∊ (−∞,−1) (wykres pochodnej narysowałem) Z wykresu widać że w −1 pochodna zmienia znak z "−" na "+" to oznacza, że −1 jest minimum

	1		1
f(−1) = −		⇒ punkt P(−1,−		) jest minimum lokalnym funkcji f(x)
	e		e

Na dzisiaj tyle starczy, możesz zrobić teraz 2 przykłady na przećwiczenie: a) f(x) = x³ * lnx b) f(x) = √x * log₂x

Godzio: Oczywiście że literówka Przepraszam chyba już zmęczony jestem, do tego jutro o 9 pobudka i na komunię kuzyna ...

Godzio:

	1
Trochę namieszałaś z tym pierwiastkiem, musisz zapamiętać, ten schemat
	2√

jest tylko przy pierwiastku kwadratowym: √x, √tgx itd. jeśli mamy większy stopień to sprowadzamy to do postaci x^... W tym wypadku: x^5/3

	5		5
Korzystamy (xn)' = nxn − 1 i mamy:		x2/3 =		3√x2
	3		3

Kejt: nie szkodzi.. ja też za chwilę skończę z twarzą na klawiaturze, więc pozwolisz, że zrobię to jutro "na świeżo". A mnie by chyba do kościoła nie wpuścili

Godzio: Ok Jutro wieczorem rozwinę trochę temat badania funkcji. Ja już idę spać bo padam, zatem do jutra i dobranoc

Kejt: dobranoc

Kejt: pochodne policzyłam.. ale dalej jest problem..

Godzio: To podaj wyniki tylko i działamy dalej

Kejt: a) x²(3 ln x + 1)

	log2x		√x
b)		+
	2√x		xln2

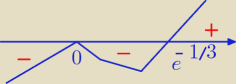
Godzio: a)D = (0,∞) f'(x) > 0 x²(3lnx + 1) > 0

	1
x = 0 lub 3lnx + 1 = 0 ⇒ lnx = −		⇒ x = e−1/3
	3

w 0 pochodna nie zmienia znaku więc to nie jest ekstremum

	1		1
f(e−1/3) = e−1 * −		= −		− ten punkt jest minimum,
	3		3e

Funkcja malejąca (0,e^−1/3) rosnąca (e^−1/3,∞)

Godzio: b) Jak liczysz monotoczność f'(x) > 0 to pomnóż przez √x bo przy naszej D √x > 0 i się sporo uprości

Kejt:

log2x		√x
	+		>0 /*√x
2√x		x ln 2

log2x		|x|
	+		>0
2		x ln 2

da się z tym coś dalej zrobić? wybacz, że się nie odzywałam.. musiałam się trochę z j.polskim pomęczyć..

Godzio: Działamy na x > 0 więc |x| = x

Kejt: ach.. tak.

Godzio: Może być trochę problem z przekształceniami więc:

log2x		1
	+		> 0
2		ln2

log₂x * ln2 + 2 > 0

	2
log2x > −
	ln2

	lne2
log2x > −
	ln2

log₂x > −log₂e² log₂x > log₂e⁻² Dalej działaj sama

Kejt: x>e⁻² coś jeszcze? dobrze, że nie siedzę obok.. bo pewnie już by mi się krzywda stała

Godzio: Jest ok To teraz podam mi maksimum bądź minimum i przedziały monotoniczności (pamiętaj o dziedzinie )

Kejt: x>e⁻² czyli miejsce zerowe to: x=e⁻² tak? i funkcja jest tylko malejąca?

Godzio: Rozwiązanie wskazuje tylko kandydata na ekstremum, Funkcja jest rosnąca dla x ∊ (e⁻²,∞) malejąca dla x ∊ (0,e⁻²) f(e⁻²) = √e⁻²log₂e⁻² ⇒ (e⁻²,√e⁻²log₂e⁻²) jest minimum Bo pochodna zmienia tam znak z − na + czyli najpierw maleje −> dochodzi do punktu (e⁻²,√e⁻²log₂e⁻²) i zaczyna rosnąć

Kejt: poddaję się.. nic z tego nie rozumiem..

Godzio: Czego dokładnie ? Dana jest funkcja f(x), liczysz jej pochodną f'(x), Jeśli f'(x) > 0 (rozwiązujesz tą nierówność i wyznaczasz x) to w danym zbiorze rozwiązań funkcja rośnie, jeśli f'(x) < 0 (tak samo) to funkcja jest malejąca w tym przedziale, gdy f'(x) = 0 to te rozwiązania są kandydatami na ekstremum, jeśli pochodna zmienia tam znak (tzn przecina oś OX) to jest to minimum lub maksimim (max gdy zmienia znak z + na −, min gdy zmienia znak z − na + )

Kejt: ech.. dasz mi jakiś łatwy przykład? spróbuję to zrobić..

Godzio:

	x2
f(x) =
	x + 1

Karola: A mógłby mi ktos pomóc?

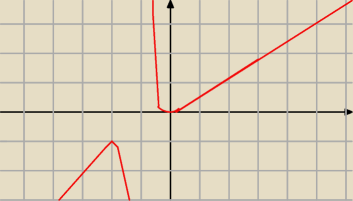
Kejt: no i mam.

	x(x+2)
f'(x)=		(wykres, taki mniej więcej, jest na górze)
	(x+1)2

rozwiązuję nierówność:

x(x+2)
	>0
(x+1)2

wychodzi: rosnąca dla: x∊(−∞;−2)u(0;+∞) malejąca dla: (−2;0) f'(x)=0 <=> x∊{0;−2} no i teraz przy −2 w ogóle nie styka się z osią Ox a przy 0 nie zmienia znaku.. cały czas jest na plusie oprócz tego gdy x=0 co teraz? nie ma ekstremum?

b.: wykres jest niedobry: f' jest (jak sama niżej policzyłaś) dodatnia dla x∊(−∞;−2)u(0;+∞) , w x=−2 ma zero, x=−1 jest asymptotą pionową obustronną inna rzecz: z tego, że f'(x)>0 dla x∊(−∞;−2)u(0;+∞) NIE WYNIKA, że f jest rosnąca na (−∞;−2)u(0;+∞) ! (to jest częsty błąd)

b.: aha sorry, to jest wykres f, może jest dobry

Kejt: zgubiłam się..

Kejt: ech.. i tak.. wykres jest zły.. zapomniałam, że mianownik jest do kwadratu..

Grześ: Chodzi Ci że w sumie przedziałów nie jest rosnąca, lecz należy zapisać, że: f rosnąca dla x∊(−∞,−2) x∊(0,+∞) Rosnąca przedziałami, ale nie w sumie przedziałów. Zapewne o to chodziło

Grześ: Czasem tak się zdarza, lecz trzebaby było dokładnie sprawdzić wartości, co zaraz uczynię Czyli wartości: f(0)=0 f(−2)=−4 Po sprawdzeniu wartości w tych punktach na początku możnabyło wątpić w tą tezę, lecz ogłaszam wszem i wobec, że można zapisać sumę tych przedziałów Amen

Godzio: Co do tego wykresu pochodnej to nie trzeba takiego dokładnego Chodzi o to żeby odczytać z niego przedziały monotoniczności i ekstrema, Tak jak się rysuje "fale" w nierównościach wielomianowych tylko że tam odczytujemy zbiór rozwiązań

Kejt: tak czy siak.. muszę go jeszcze raz narysować.. przez ten wstrętny kwadrat w mianowniku..

Godzio: Spokojnie to dopiero początki, jak to załapiesz to przechodzimy poziom wyżej, czyli wypukłość funkcji i punkty przegięcia

Godzio:

	x2
f(x) =
	x + 1

D = R − {−1} − o tym też pamiętać

	2x(x + 1) − x2		x2 + 2x		x(x + 2)
f'(x) =		=		=
	(x + 1)2		(x + 1)2		(x + 1)2

f'(x) > 0 x(x + 2) > 0 f↗ x ∊ (−∞,−2),(0,∞) f'(x) < 0 ⇒ f ↘ x∊(−2,−1),(−1,0)

	4
f'(x) = 0 ⇒ x = −2 lub x = 0 , f(−2) =		= −4, f(0) = 0
	−1

Teraz powiedz mi co jest minimum a co maksimum ?

Godzio: Po tym zrób jeszcze taki przykład:

	x2 + 2
f(x) =
	x2 − 1

Jak zrobisz go dobrze to przejdziemy powoli dalej, teraz wychodzę, będę później to sprawdzę

Kejt: maksimum: −2 minimum: 0

Kejt:

	x2 + 2
f(x) =
	x2−1

	−6x
f'(x) =
	(x2−1)2

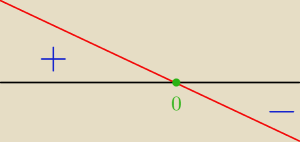
D = R − { −1 ; 1 } f'(x)>0 x<0 ekstremum może być tylko w 0 i jest to maksimum, bo zmienia znak z + na − jeśli to jest źle.. to ja się poddaję i idę spać..

Kejt: jak wrócisz mógłbyś mi jeszcze jakieś przykłady podać? mam jutro matematykę to bym sobie porobiła..bo umrę z nudów..

Godzio: Jest ok Tylko pamiętać, że dokładnie mi określać tą monotoniczność: f↗ x ∊ (−∞,−1)U(−1,0) f↘ x ∊ (0,1)U(1,∞) I maksimum to nie sam x tylko punkt (0,−2)

Godzio: 1) f(x) = x³ * e^x 2) f(x) = lnx² + x 3) f(x) = 2x⁴ − 3x² + 2x − 4 To na nudy Dobra to teraz dalsza część, tzn. jak badamy wypukłość i wklęsłość ? Liczmy druga pochodną f''(x) Gdy f''(x) > 0 ⇒ x ∊ ... funkcja jest wypukła w przedziale ... Gdy f''(x) < 0 ⇒ x ∊ ... funkcja jest wklęsła w przedziale ... Gdy f''(x) = 0 ⇒ x = ... Punkt (x,f(x) ) jest punktem przegięcia funkcji f(x)

Gustlik: Sorki, że sie wepchnnę, ale ma parę fajnych zadanek z pochodnych. Kto się podejmie? Godzio, dasz radę? Ja oczywiście metodę znam, tylko czekam na odpowiedź. 1. f(x)=x^x 2. f(x)=(sinx)^cosx 3. f(x)=(tgx)^lnx

Godzio: Zdaje się że zamienia się to do "e" f(x) = x^x = e^lnxx = e^{x * lnx} f'(x) = e^{x * lnx} * (lnx + 1) = x^x * lnx + x^x Dobrze myślę?

b.: f↗ x ∊ (−∞,−1)U(−1,0) −− nieprawda! prawdą jest natomiast, że f rośnie na (−∞,−1), a także rośnie na (−1,0) −− zrób rysunek...

b.: właśnie, dokładnie mi określać tą monotoniczność to też jest nieprawdą: f↘ x ∊ (0,1)U(1,∞)

b.: twierdzenie: jeśli f jest różniczkowalna na przedziale (a,b) oraz f'(x)>0 dla x∊(a,b), to f jest rosnąca na (a,b) nie ma takiego twierdzenia dla sumy przedziałów w miejsce przedziału (a,b)