Wyznacz wzór funkcji kwadratowej. madzia243: Proszę o pomoc w rozwiązaniu tego zadania Wyznacz wzór funkcji kwadratowej f(x)=ax²+bx+c , wiedząc, że zbiorem rozwiązań nierówności f(x)>1 jest przedział (−1;3), a największa wartość funkcji jest równa 4. Liczę że ktoś mi pomoże Czekam na odpowiedź. Pozdrawiam

Popiel: według ciebie funkcja jest roznąca czy malejąca ?

Popiel: kurde złe pytanie. Czy ramoniona funkcji skierowane są w dół czy w górę

WiemZeNicNieWiem: pewa że do góry

Popiel: w dół największa wartość funkcji jest równa 4

TOmek: oczywiscie ,ze w doł

WiemZeNicNieWiem: a jak to dalej ruszyć, weź popiel napisz rozwiązanie

Popiel: narysuje wam rysunek może się kapniecie

Grześ: z nierównoiści wynika: f(x)>1 przedział (−1,3), czyli: f(−1)=1 f(3)=1 a−b+c=1 9a+3b+c=1 8a+4b=0 2a+b=0 b=−2a, c=1−3a podstawiamy: f(x)=ax²−2ax+1−3a Liczymy wierzchołek:

	−2a
xw=		=1
	−2a

f(1)=a−2a+1−3a=−4a+1 f(1)=4 −4a+1=4

	3
a=−
	4

Czyli wzór:

	3		3		5
f(x)=−		x2+		x−
	4		2		4

Chyba nie popełniłem nigdzie błedu rachunkowego

Popiel: kurna Grześ

Grześ: Sprawdźcie chociaż warunki, albo sprawdźcie z końcową funkcją, czy spełnia warunki zadania

WiemZeNicNieWiem: nie rozumiem człowieku z tego nic, skąd takie się bierze, ze a−b+c=1 i w ogóle

arek: Takiego zadania na matmie to nie będzie dzięki Bogu.

WiemZeNicNieWiem: to jest na rozszerzenie?

Grześ: widze błąd, na końcu z pośpiechu źle zmieniłem znak wyraz wolny powinien być inny

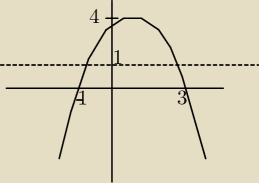
Popiel: (3−1)/2 = 1 i mamy p

Grześ:

	3		3		13
f(x)=−		x2+		x+
	4		2		4

Teraz dobrze

x-Lon: Patrzę w notatki i takiego naprawdę nie będzie zadania, nie martwcie się. Jutro będą łatwe zadania.

Popiel: Grześ pochwal się tym zapisem a+b = 1 + b

Popiel: a+c = 1 + b *

Grześ: w jakim sensie sie pochwalić

Grześ: Sprawdzałem wzór funkcji do tyłu i spełnia warunki zadania

Popiel: za cholere nie wiem co to znaczy l

Grześ: patrz masz funkcję: f(x)=ax²+bx+c masz z warunku w zadaniu: f(−1)=1 oraz f(3)=1, czyli: f(−1)=a(−1)²+b(−1)+c=a−b+c f(3)=a(3)²+b(3)+c=9a²+3b+c Rozumiemy

Popiel: wiem wiem

Popiel: innego sposobu już chyba nie ma co ?

Grześ: Widzę, że możnaby jeszcze to troszkę uprościć, dajcie chwilkę

Popiel: Odrazu na kanoniczną może ?

Popiel: nie w sumie jak wyliczysz a to b i c też będziesz miał. Z resztą ty pewnie coś wymyślisz

Grześ: mamy f(x)>1 i rozwiązanie przedzału (−1,3) Znajdujemy środek przedział€, który jest symetrią paraboli, a zarazem jego przesunięciem

3−1
	=1, to jest nasze p=1
2

Mamy dane, że max wartość jest "4", więc to jest nasze q=4 Czyli funkcja przedstawia się następujaco: f(x)=a(x−1)²+4, teraz wykorzystujemy dowolny z warunków, np. f(−1)=1, czyli: 1=a(−1−1)²+4 −3=a*4

	3
a=−		, podstawiamy:
	4

	3
f(x)=−		(x−1)2+4, teraz tylko wymnożyć do postaci ogólnej
	4

madzia243: całuski dla Grzesia

Grześ: Hehe.. niepotrzebnie Bierz się do pracy i tyle Powodzenia

Grześ: I jak myślicie Chyba dośc szybszy był ten drugi sposób

Popiel: no z pewnością szybszy od pierwszego

Grześ: wieeem... poleciałem od razu w układy równań.. mnie one nie przeszkadzają, bo niezbyt skomplikowane.. Ale jednak lepsza analiza paraboli jest Bynajmniej mozna sposób wybrać

Popiel: zawsze najlepiej jest sobie wyobrazić jak ta parabola będzie szła

Piermazon: Dupa mnie boli