Kilka pytań. Matt: Czy ja mogę tak zrobić:

2√3		2		2√7
	=		=
√21		√7		7

i ile rozwiązań ma:

x
	= 0
x(x+2)

Matura jutro, wyjaśniam sprawy które sa nie jasne

bump: 1) nie mozesz

bump: 2) zero

Marta: a w 2) przypadkiem nie jest jedno rozwiązanie? wtedy gdy x ∊ {0}

bump: 2) jako ze mianownik nie moze byc rowny 0 to z dziedziny wykluczamy 0 i −2 bo rowanie x(x+2) gdy podstawimy 0 lub −2 daje nam wynik 0 w takim razie jesli cale rownanie ktore podales ma rownac sie zero to licznik musi byc rowny 0 a to oznacza ze niby x powinien byc zerem ale wczesniej wykluczyles 0 z dziedziny wiec nie moze byc dlatego nie ma

Nie jestem mądry: x sie skróci z tym na dole i będziesz miała 1=0 co nie jest prawdziwe

Kejt: ale przecież..

2√3		2√3		2		√7		2√7
	=		=		*		=
√21		√3*√7		√7		√7		7

coś źle..?

bump: Kejt Jesli piszesz ze jest dobrze to tak jest xD

Vax: Dokładnie, w 1 tak można.

Któś: NIE Tak nie można! W ten sposób zrób:

2√3		2√3*√21		2√3*21		2√63		2√9*7
	=		=		=		=		=
√21		√21*√21		21		21		21

2*3√7		2√7
	=
21		7

wprawdzie ten sam wynik ale za to otrzymasz maksa a za tamto 0 pkt

Któś: NIE Tak nie można! W ten sposób zrób:

2√3		2√3*√21		2√3*21		2√63		2√9*7
	=		=		=		=		=
√21		√21*√21		21		21		21

2*3√7		2√7
	=
21		7

wprawdzie ten sam wynik ale za to otrzymasz maksa a za tamto 0 pkt

Wojteq66: usuwasz niewymiernosc, wiec

2√3		2√3 *√21		√63
	=		=
√21		√21*√21		7

Wojteq66: tfu zle spojrzalem tam 2 jest!

Kejt: 2. trzeba określić dziedzinę: x(x+2)≠0 x≠0 ⋀ x+2≠0 x≠−2 czyli: D∊R−{0;−2} rozwiązujemy równanie:

x
	=0 /*[x(x+2)]
x(x+2)

x=0 x∉D więc równanie nie ma rozwiązań.

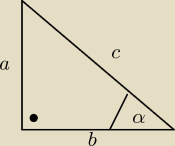
Matt: a= 2√3 b=3 więc 12+9=21 wiec c = √21

	2√3
wiec sin =
	√21

a nie ma takiej odp, za to jest

2√7
7

Vax: Widać, że niektórzy myślą schematami wykutymi na pamięć nie rozumiejąc, na czym to polega, sposób podany w 1 poście jest jak najbardziej poprawny, za niego dostałoby się z pewnością maksymalną ilość punktów.

ICSP: można tak zrobić i przestań ze dostanie 0.

Marta: ehmm. racja. Jestem chyba w gorącej wodzie kąpana chyba bo wszystko robie szybko i nie zauważam ważnych rzeczy

Vax:

	2√3		2√7
@Matt, przecież		=
	√21		7

Matt: Cześć Kasiu I cześć wszystkim Czyli dzielenie pierwiastków odpada, tak? ;> A takie coś.. Jakie rozwiązania ma parabola jeśli ma ramiona do góry i jest ponad osią OX w zależności od < i > ? I jakie ma jeśli lezy poniżej OX i ma ramiona w dół? Jak to zależy od < i > ?

Matt: Ej to wkońcu jak z tym dzieleniem pierwistków?

Kejt: Cześć Macie Jeśli chodzi Ci dokładnie o ten sposób, którym Ty robiłeś i ja w pierwszym zadaniu to jest on jak najbardziej poprawny

Matt: Rewelacja! Macie hehe, Mateusz zmieniłem z Mati sobie haha A jak z tymi parabolami? O i jeszcze takie coś − mamy ciąg arytmetyczny z a₁ = −3 a a₁45=2157 wiec robie sobie: −3 + 144r = 2157 144r=2160 r=15 ?;>

Vax: Korzystamy z tego, że a_n = a₁+(n−1)*r mamy istotnie a₁₄₅ = a₁+144r = −3+144r czyli −3+144r = 2157 ⇔ r=15 Pozdrawiam.

Matt: Hmm, ok A b₈ = 2√2, jest to ciąg geometryczny o ilorazie ⁶√2 więc wyraz b₁ to?;>

Matt: Funkcję która ma zbiór wartości <−2, 3> przesuwamy o 2010 w górę, to ona ma wartości <2008, 2014> ?

Vax: 1) 2^3/2 = b₈ = b₁*q⁷ = b₁*2^7/6 skąd wynika b₁ = 2^1/3 2) Nie, Skoro Zw = [−2;3] to przesuwając o 2010 w górę mamy [−2+2010;3+2010] = [2008;2013]

Matt: Zbadaj czy istnieje taka wartość współczynnika a dla której wielomiany w(X) i q(x)² są równe jeśli Q() = x² + ax −1 W(x) = x⁴ + 2x²+x²−2x+1 To ja mam po prosotu podnieść do kwadratu Q(x) i sprawdzić wspólczynniki w obu wielomianach? Bo jeśli to wg, mnie nie ma takiego a. Mógby ktoś zrobic u siebie to? ;>

Matt: Dzięi Vax

Kejt: nie lubię trójmianów kwadratowych podnosić do kwadratu.. jeśli to zrobisz to Ci to policzę

Matt: (x² + ax −1)(x² + ax −1) = a⁴ +ax³−x²+ax³+a²x² − ax −x² −ax + 1 ;>