Zbiór rozwiązań nierownosci

Zbiór rozwiązań nierownosci P: Zbiór rozwiązań nierownosci |x−3|≥1 . Jak bedzie wygladal przedzial ?

4 maj 14:27

Kejt: |x−3|≥1 x−3≥1 ⋀ x−3≤−1 x≥4 ⋀ x≤2 x∊(−∞;2>∪<4;+∞) chyba tak.

4 maj 14:30

P: aha , dość łatwy sposób emotka

zawsze można rozwiązywać tak nierownosc ?

4 maj 14:32

Kejt: z wartością bezwzględną tak.. pod warunkiem, że występuje ona w takiej postaci.. a nie np.: |x−1|+|x+4|>1

4 maj 14:33

P: a jak by tak wygladala to czemu nie mozna ?

4 maj 14:34

adam:

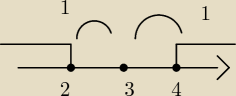
|x−3|=0 x−3=0 x=3 x e(−∞, 2> u <4, +∞) SORY ZA WYKONANIE

4 maj 14:34

Kejt: bo masz dwa przedziały, nie jeden.

4 maj 14:35

P: 7^4³x³√7⁵

4 maj 14:36

P: aha aha to juz kumam. A jak rozwiązać to ?

4 maj 14:36

Kejt: x to znak mnożenia?

4 maj 14:39

;): Lub jeżeli chcesz się dłużej bawić to możesz zrobić √(x − 3)² ≥ 1 /² x² − 6x + 8 ≥ 0 x₁ = 2 x₂ = 4 x ∊ (−∞,−2>∪<4,∞)

4 maj 14:40

P: tak x to mnozenie emotka

Dzieki buzka ale potrzebuje szybkie i proste sposoby

4 maj 14:42

Kejt: 7⁴³ * ³√7⁵=7¹² * 7^⁵₃ = 7^{12 + ⁵₃}=7^{³⁶₃ + ⁵₃} = 7^⁴¹₃

4 maj 14:43

P: a dlaczego wyszło Ci 7¹²

4 maj 14:45

P: nie wiem czy dobrze napisalem bo tam jest 7 do potegi ⁴₃

4 maj 14:49

P: 4/3

4 maj 14:49

Kejt: no to źle napisałeś..bo zrobiłeś dwie potęgi.. 7^⁴₃ * 7^⁵₃=7^{⁴₃ + ⁵₃} = 7^⁹₃= 7³

4 maj 14:54

P: aha , zastanawialo mnie jak zrobic potege z tym pierwiastkiem emotka

4 maj 14:57

P: Pewien wiloscian na 6 krawedzi. Liczba jego scian jest rowna ?

4 maj 14:58

Eta: 4

4 maj 15:02

P: a jak to sie liczy ? jest wzor jakis czy trzeba to sobie narysowac ?

4 maj 15:04

P: a jak to sie liczy ? jest wzor jakis czy trzeba to sobie narysowac ?

4 maj 15:05

4 maj 15:13

Slannesh: a takie cuś? Bo nie wychodzi mi . 3,2x<1³₅

3 sty 17:10

Slannesh: przedzial tej nierownosci to (−∞:−0,2)

3 sty 17:11