Ilę rozwiązań rzeczywistych
Ewa: Ilę rozwiązań rzeczywistych ma równanie 5x4−13=0
Zgóry dziękuje za pomoc
4 maj 10:02
Vax: Zauważ, że f'(x) = 20x3 ⇒ f'(x) = 0 ⇔ x = 0, skoro pochodna funkcji ma jedno miejsce zerowe
dana funkcja ma maksymalnie 2, zauważamy, że:
f(−2) > 0 , f(−1) < 0 , f(1) < 0 , f(2) > 0 czyli z tw. Darboux wynika, że funkcja posiada 2
pierwiastki w przedziałach (−2;−1) oraz (1;2)
Pozdrawiam.
PS. Można też skorzystać ze wzoru skróconego mnożenia.
4 maj 10:16
Bogdan:
5x
4 − 13 = 0 ⇒ 5x
4 = 13
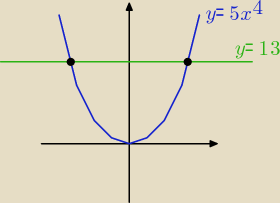
y = 5x
4 i y = 13
Widać liczbę rozwiazań równania.
4 maj 10:50
 5x4 − 13 = 0 ⇒ 5x4 = 13
y = 5x4 i y = 13
Widać liczbę rozwiazań równania.
5x4 − 13 = 0 ⇒ 5x4 = 13
y = 5x4 i y = 13
Widać liczbę rozwiazań równania.