awdawdawdad
karol: Dla jakich wartości parametru m równanie (m−1)x2−2mx+m−2=0 ma dwa róźne pierwiastki dodatnie.
założenia
a≠0
Δ>0
x1x2>0
x1+x2>0
Δ=12m −8
Δ>0 <=> m>2/3
a≠0<=> m∊R − {1}
x1x1= m−2m−1
x1x1>0<=> −1>0 więc x∊∅
Czy dobrze to policzyłem ? Mógłby ktoś to sprawdzić ?
3 maj 19:53
karol:
3 maj 20:00
Nie jestem mądry: Dobrze
3 maj 20:05
Nie jestem mądry: Tylko nie rozumiem skąd to x1x2>0
3 maj 20:07
Nie jestem mądry: a już wiem

3 maj 20:07
karol : aż się zdziwiłem, ze dobrze

3 maj 21:06
karol : ale czy to jest napewno dobrze, bo wtedy połowa zadania nie ma sensu...
3 maj 21:13
karol :
3 maj 21:21
karol :
3 maj 21:35
karol :
3 maj 21:35
karol :
3 maj 21:54
sd: m−1≠0 jeszcze
3 maj 21:57
karol : ale wynik jest dobry ? x1x2>0<=> −1>0 więc x∊∅ ? Dobrze jest to policzone ?
3 maj 22:26
karol :
3 maj 22:34
Kosmos: dobrze wyszło

3 maj 22:36
Kosmos:
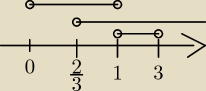
3 maj 22:37
karol : Jeżeli dobrze wyszło, to ostatecnza odpowiedzią jest, że nie ma rozwiązania, tak ?
3 maj 23:01
karol :
3 maj 23:10
karol :
3 maj 23:26
karol :
4 maj 00:29
karol :
4 maj 00:34
karol :
4 maj 00:38
karol :
4 maj 11:35
karol :
4 maj 14:56
ICSP:
4 maj 15:10



