zadania < Grzegorz >: 1) W ostrokątnym trójkącie równoramiennym ramię ma długość 61, a wysokość poprowadzona do ramienia ma długość 11. a) oblicz pole tego trójkąta b) oblicz długość podstawy tego trójkąta 2) Ciąg ( an) określony jest wzorem an=n2+20n+4 a) oblicz dziesiąty wyraz ciągu (an) b) o ile procent trzeci wyraz ciągu (an) jest większy od wyrazu drugiego? 3) Ciąg (an) określony jest wzorem an =−2n+5 a) uzasadnij ( na podstawie definicji), że ciąg (an) jest arytmetyczny b) suma ilu początkowych wyrazów ciągu (an) jest równa −14 c) określ monotoniczność ciągu (an). 4) Iloraz ciągu geometrycznego (an) równy jest 3, a suma odwrotności wyrazu pierwszego i drugiego wynosi 18 a) oblicz pierwszy wyraz ciągu (an) b) podaj wzór ogólny ciągu (an)

< Grzegorz >: Błagam pomocy ! 1) W ostrokątnym trójkącie równoramiennym ramię ma długość 61, a wysokość poprowadzona do ramienia ma długość 11. a) oblicz pole tego trójkąta b) oblicz długość podstawy tego trójkąta 2) Ciąg ( an) określony jest wzorem an=n²+20n+4 a) oblicz dziesiąty wyraz ciągu (an) b) o ile procent trzeci wyraz ciągu (an) jest większy od wyrazu drugiego? 3) Ciąg (an) określony jest wzorem an =−2n+5 a) uzasadnij ( na podstawie definicji), że ciąg (an) jest arytmetyczny b) suma ilu początkowych wyrazów ciągu (an) jest równa −14 c) określ monotoniczność ciągu (an). 4) Iloraz ciągu geometrycznego (an) równy jest 3, a suma odwrotności wyrazu pierwszego i drugiego wynosi 18 a) oblicz pierwszy wyraz ciągu (an) b) podaj wzór ogólny ciągu (an)

< Grzegorz >: Kto mi pomoże w tych zadaniach

Nie jestem mądry: No postaram się pomóc

Nie jestem mądry: No to postaram się pomóc

Nie jestem mądry: Zad. 1 a) Wzór na pole : P= ¹₂a*h a mamy podane a=61 h=11 Więc : P= ¹₂*61*11

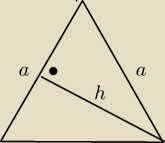
Nie jestem mądry: Zad.1 b) AC=BC=61 BD=11 Wyliczymy długość DC z tw.Pitagorasa: DC²=BC²−DB²=3721−121=3600 ⇒ DC=60 Po obliczeniu DC możemy obliczyć długość odcinka AD AD = AC−DC=61−60=1 Z trójkąta ABD wyliczamy długość podstawy AB trójkąta ABC AB²=AD²+ DB²= 1+ 121=122 ⇒ AB = √122

Kuba: Zad 4. q=3

1		1
	+		=18
a1		a2

	a2+a1
a)		=18
	a1*a2

(a1*q)+a1
	=18
a1*a1*q

3a1+a1
	=18
a1*3a1

4a1
	=18
(3a1)2

4
	=18 /*a1
3a1

4=54a₁ a₁=4/54 =2/27 Dziwnie wyszło? Pewnie źle a_n=2/27*3ⁿ

Nie jestem mądry: Zad.2 a) a_n=n²+20n+4 Żeby obliczyć dziesiąty wyraz ciągu w miejsce n wstawiamy 10 a₁₀=10²+20*10+4=100+200+4=304 b) Liczymy drugi oraz trzeci wyraz ciągu: a₂= 4+40+4=48 a₃= 9+60+4=73 Teraz układamy proporcje : 48 −−−− 100% 25 −−−− x% ⇒ x ≈52% czyli trzeci wyraz to ≈ 152% drugiego

< Grzegorz >: próbowałem to 2 zrobić wyszło mi prawie tak samo , a to zad. 4 to nie wiem bo tego nie rozumie . Mam nadzieję że znajdzie się jeszcze ktoś kto mi pomoże to dla mnie bardzo ważne

Nie jestem mądry: Zad. 4 wyraz pierwszy ciągu zaznaczamy jako x stąd 2 wyraz to 3x bo q=3 Suma odwrotności czyli ¹_x+¹_3x=18

3+1
	=18
3x

⁴_3x=18 4=54x ⇒ x= 13¹₂ czyli a₁=13¹₂ a_n= 13¹₂* 3ⁿ⁻¹

< Grzegorz >: przepraszam pomyliłem się chodziło mi o zad 1 a napisałem 2 to 1 wyszło mi podobnie a pozostałych nie umie sobie sam zrobić liczę na Waszą pomoc

Kuba: W życiu twoim całym 54x=4 to x≠54/4 tylko x=4/54

Nie jestem mądry: A Rzeczywiście przepraszam śpieszyłem się

Nie jestem mądry: To już naprawiam błąd 54x=4 ⇒ x= ⁴₅₄= ²₂₇ a_n= ²₂₇* 3⁽n−1) Chyba już bez błędów

Nie jestem mądry: Zad.3 a) Wystarczy wykazać że różnicą wyrazów a{n+1) i a_n jest jakaś liczba rzeczywista Czyli : a_n= −2n+5 a_n+1=−2(n+1)+5 (w miejsce n wpisujemy n+1) =− 2n+7 a_n+1−a_n= −2n+7 −( −2n+5)= −2n+7+2n−5=2 Więc ciąg jest arytmetyczny , liczba 2 jest różnicą tego ciągu

< Grzegorz >: przepraszam bardzo ale mógłbym poprosić jeszcze o rozwiązanie zad.3

< Grzegorz >: to są już całe rozwiązania tych zadań ?

Nie jestem mądry: Zad.3 b) Wzór na sumę n początkowych wyrazów w ciągu arytmetycznym :

	2a1+(n−1)r
Sn=		*n
	2

Wyliczamy pierwszy wyraz ciągu: a₁=−2*1+5=3 r=2

	6+3n−3
−14=		*n
	2

i wyliczasz z tego n

Nie jestem mądry: Zad.3 c) policz a₁ a₂ i a₃ i zobaczysz czy ciąg jest rosnący czy malejący a może stały

Nie jestem mądry: Jeśli coś jest niezrozumiałe chętnie wytłumaczę

< Grzegorz >: Nie jestem mądry : przepraszam że o to pytam ale która to liczba a₂, i a₃ w zad.3

Nie jestem mądry: Podstawiasz do wzoru a_n= −2n+5 w miejsce literki n 2 chcąc znalezć 2 wyraz ciągu lub 3 gdy szukasz trzeci wyraz ciągu i wtedy otrzymasz: a₂= −2(2)+5 a₃= −2(3)+5

Nie jestem mądry: Znalazłem błąd u siebie ZAd.3 a)

< Grzegorz >: aha ale jestem głupi Bardzo Ci dziękuję za pomoc

< Grzegorz >: jaki?

Nie jestem mądry: a_n+1=−2(n+1)+5=−2n+3 Więc będzie tak: a_n+1− a_n= −2n+3−(−2n+5)=−2n+3+2n−5= −2 ⇒ r= −2 i ciąg jest malejący. Przepraszam za błąd za bardzo się śpieszę

bump: w koncu nie jestes madry

Nie jestem mądry:

	6−2n+2
wtedy Sn=		*n
	2

Teraz już wszystko dobrze Za bardzo się śpiesz ę dlatego robię błędy a a nick nie mówi nic o mnie

< Grzegorz >: Jeszcze raz Ci bardzo dziękuję za pomoc Na podstawie Twoich rozwiązań uczę się to rozwiązywać bardzo bardzo dziękuję

Nie jestem mądry: Nie ma za co

Nie jestem mądry: Nie ma za co

< Grzegorz >: Słuchaj do Nie jestem mądry: powiedz mi prosze skąd Ci wyszło w zad.3b 48−−−100% 25−−−x% jak a₂=48 a₃=73 tego nie rozumie bardzo proszę o odpowiedz

< Grzegorz >: lub jak ktoś inny jest mi chętny pomóc w tym rozumowaniu to bardzo proszę o szybką odpowiedz

Kosmos: 2b ?

< Grzegorz >: tak

< Grzegorz >: to jak jest z tym rozwiązaniem

Kosmos: Napiszę ci jak ja robię zadania typu O ile procent może się przyda Np. O ile procent a= 64 jest większe od b= 16 Pierwsze co robię to licze różnicę tych liczb c = 64−16 = 48 I teraz czytam jeszcze raz polecenie W poleceniu jest O ile procent liczba a jest WIĘKSZA od b czyli układam równanie: x%*b = c, czyli x%*16=48 zawsze różnicę daję do środka. I teraz dlaczego takie równanie, bo 48+16 = 64 Gdyby było O ile mniejsza to wtedy x%*16=64 bo 64 − 16 = 48 Rozumiesz ?

Kosmos: różnica na zewnątrz* dobrze jest a źle napisałem

Kosmos: kurde ale jaj sam się pogubiłem w tym co napisałem Napisze to jeszcze raz( jak sam zauważyłeś błąd to dobrze ) O ile procent a = 64 jest większe od b = 16 Różnica c = 64 − 16 = 48 x%*16 = 48 bo 16+48 = 64 O ile procent b = 16 jest mniejsze od a = 64 Różnica c= 64−16 = 48 x%*64 = 48 bo 64−48 = 16 Teraz Ok i sory że zagmatwałem

< Grzegorz >: czyli z mojego zadania trzeci wyraz to jest w przybliżeniu 152% drugiego wyrazu ?

< Grzegorz >: chodzi mi o zadanie 2.

< Grzegorz >: trochę mi teraz namieszałeś i się całkiem pogubiłem

Kosmos: nie 152% to byś miał cały ten wyraz + jeszcze 52 jak byś się nauczył mojego sposobu było by ci dużo łatwiej myślę. Jeszcze raz sory za zamieszanie teraz jest dobrze

< Grzegorz >: napisz mi czy ten wynik Ci wyszedł tak samo , bo nie wiem czy ma być 152%

Kosmos: ma być 52% w przybliżeniu

< Grzegorz >: no to jak wreszcie powinno być ? zapisane jest tak , ale wychodzi na to że powinno być x%−−−−−−73 a nie 25 48−−−100% 25−−−x% jak a2=48 a3=73

< Grzegorz >: tak wiem ale cały czas chodzi mi o ile % trzeci wyraz ciągu (a_n) jest większy od wyrazu drugiego ?

Kosmos: tak ale od 152% odejmij 100% i ci wyjdzie 52%

Kosmos: aaa o to ci chodzi te 25 to jest właśnie różnica i teraz ci wyjdzie czysto 52%

< Grzegorz >: wyżej w zadaniach jak zauważyłeś mam napisane 152% i to mnie myli już sam zgłupiałem

Kosmos: to jest dokładnie to samo co ci wyżej napisałem

< Grzegorz >: czyli dobrze będzie zapisane jak będzie 25−−−−x% a nie jak myślałem że ma być 73−−−x%

Kosmos: to i to jest dobrze tylko jak zapiszesz 73 to będziesz musiał na końcu odjąć 100% a jak zapiszesz 25 to dostaniesz odrazu wynik bo 25 stanowi 52% liczby 48

< Grzegorz >: no dobra wiem że jestem mało kumaty ale zależy mi żeby dobrze to zrozumieć , mam jeszcze pytania do zad.3 tylko nie wiem czy mi chcesz pomóc

< Grzegorz >: jak w zad. 3 wylicza się liczbę n

< Grzegorz >: treść zadania jest taka 3) Ciąg (an) określony jest wzorem an =−2n+5 a) uzasadnij ( na podstawie definicji), że ciąg (an) jest arytmetyczny b) suma ilu początkowych wyrazów ciągu (an) jest równa −14 c) określ monotoniczność ciągu (an).

Kosmos: co chesz zrobić napisz

Kosmos: a) Uzasadnij na podstawie definicji czyli musisz sprawdzić czy r nie zależy od n różnica musi ci wyjść stała b) Po prostu wzór na sumę i przyrównujesz do −14 c) sprawdzasz jaka jest różnica jeżeli r < 0 to ciąg malejący r > 0 rosnący r = 0 stały

< Grzegorz >: chodzi mi dokładnie o zad 3bi c właśnie tego nie rozumie liczę na to że Ty mi pomożesz

Kosmos: to może ty napisz jak to liczysz czy nie wiesz jak się zabrać ?

< Grzegorz >: i dokładnie napiszesz jak to ma po kolei lecieć

< Grzegorz >: no właśnie nie wiem dlatego proszę o pomoc

Kosmos: a na pewno tam ma być − 14?

< Grzegorz >: tak

< Grzegorz >: tak mam podane w zadaniach na pewno ma być −14

Kosmos: w takim razie nie ma takich n początkowych które dadzą w sumie − 14

< Grzegorz >: to jak to zadanie zapisać

Kosmos: c) bierzesz dowolne dwa wyrazy np a₁ = 3, a₂ = 1 i odejmujesz drugi od pierwszego 1−3 = −2 różnica ujemna więc ciąg malejący. A jak byś miał to zrobić na podstawie definicji to tak jak w a)

Kosmos:

	3+(−2n+5)
−14=		*n
	2

−14 = (−n+4)*n n² − 4n − 14 = 0 Δ = 72 Dziedziną ciągu sa liczby N+ więc n₁ i n₂ odpada

< Grzegorz >: jest zapisane że b) Wzór na sumę n początkowych wyrazów w ciągu arytmetycznym :

	2a1+(n−1)r
Sn=		*n
	2

Wyliczamy pierwszy wyraz ciągu: a1=−2*1+5=3 r=2

	6+3n−3
−14=		*n
	2

i wyliczasz z tego n

< Grzegorz >: wiem wiem że jest późno ale myślałem że to zrozumie i wreszcie będę miał z głowy te zadania

< Grzegorz >:

Godzio: 3) Ciąg (an) określony jest wzorem an =−2n+5 a) uzasadnij ( na podstawie definicji), że ciąg (an) jest arytmetyczny b) suma ilu początkowych wyrazów ciągu (an) jest równa −14 c) określ monotoniczność ciągu (an). o to chodzi ?

< Grzegorz >: tak

< Grzegorz >: Kto z Was pomoże mi to zrozumieć ? Bardzo bym prosił a dokładnie chodzi mi o zad.3 b) i c)

< Grzegorz >: Pomóżcie proszę bardzo Was proszę