vbv b
Maturzystka: Punkty A=(2,0) i B=(12,0) sa wierzcholkami trojkata prostokatnego ABC o przeciwprostokatnej AB.
Wierzcholek C lezy na prostej o rownaniu y=x. Oblicz wspolrzedne punktu C
2 maj 22:59
ICSP: (3;3)
(4;4)
2 maj 23:06
SzymeQ: C=(3,3)
2 maj 23:07
Maturzystka: Mhmmm.......a skąd to ?;> moze jakies rozwiazanie?
2 maj 23:08
SzymeQ: Sorry
C=(2,2)
2 maj 23:08
SzymeQ: rysunek i nic więcej
2 maj 23:09
Ireneusz: Oblicz odcinek AB AC BC. I później z pitagorasa policzysz. Współrzędne punktu c(x,x)
2 maj 23:09
ICSP: no właśnie szymeq zrób sobie rysunek wyjdzie ci trójkąt sferyczny.
2 maj 23:09
Maturzystka: jak z pitagorasa?
2 maj 23:09
ICSP: rozwiąż układ równań:
y = x
(x−7)2 + y2 = 25
2 maj 23:11
Ireneusz: Albo inaczej... można obliczyć to ze równania okręgu i tej prostej. Chyba tak łatwiej będzie.
Gdzieś już to zadanie robiłem...
2 maj 23:11
SzymeQ:
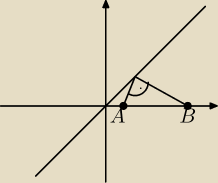
No z rysunku to szybko odczytasz, bo rozwiązywanie trochę zajmie
2 maj 23:11
SzymeQ: Masz odpowiedzi do tego
2 maj 23:12
Ireneusz: Maturzystko z tej pierwszej metody jak policzysz kwadraty boków, to powinno wyjść równanie
kwadratowe z którego wyjdą te współrzędne.
2 maj 23:13
Ireneusz: Ale SzymeQ. Tutaj będą 2 odpowiedzi
2 maj 23:13
ICSP: mam
C(3;3)
C(4;4)
dwa rozwiązania.
2 maj 23:13
Eta:
Środek okręgu opisanego na Δ ABC S ( 7,0) |AB\ =10
to: r= |AS|= |SB| = ISC|=5
C(x,x)
o : ( x −7)2 +x2= 25
Rozwiązując to równanie otrzymujemy x= 3 v x= 4
2 maj 23:14
ICSP: Eto to samo napisałem wyżej
2 maj 23:15
Maturzystka: Wrr.... dajcie jakies jedno, całe rozwiazanie co?
2 maj 23:15
SzymeQ: i właśnie to mnie w matmie zadziwia jak narysujesz i użyjesz ekierki,
albo na maturze nie można ekierki to cyrkiel i konstrukcyjnie kąt w
yznaczysz i to 3,3 nie ma kąta prostego, ani 4,4 nie ma kąta prostego
2 maj 23:15
Eta:
Sorry, jak pisałam , to nie widziałam Twojego wpisu .......
2 maj 23:16
ICSP: przecież się nie obrażę
2 maj 23:17
Eta:
Ufff
2 maj 23:18