pole obszaru ola: Oblicz pole powierzchni obszaru zawartego pomiędzy y=x²−1 oraz y=x+1. Narysuj ten obszar.

Grześ: Znów pomóc?

SzymeQ: grześ dawaj

Grześ: daruje sobie rysunek, bo spieszy mi się, już to zapisze

SzymeQ: no to ciekawe jest, ola to oddajesz do szkoły babce do spr czy to dla siebie do matury robisz

bart: SzymeQ to juz sa studia

Grześ: znajduję punkty przecięcia: x²−1=x+1 x²−x−2=0 (x−2)(x+1)= x=2 lub x=−1 y=3 lub y=0 Czyli mamy punkty przecięcia (−1,0) oraz (2,3), Teraz podstawmy dowolny argument z przedziału (−1,2) i sprawdźmy która funkcja jest wyższa: f(1)=1−1 g(1)=1+1=2 Widać, że funkcja liniowa jest wyższa, czyli liczymy całkę: 2 2

	1		1
∫ (x+1−x2+1) = ∫ (−x2+x+2) = [−		x3+		x2+2x]−12 =
	3		2

−1 −1

	8		1		1		1		1		1
=(−		+2+4)−(		+		−2)=3		+1		=4		j2
	3		3		2		3		6		2

SzymeQ: wiem dlatego się pytam Oli czy to oddaje babce, czy nie bo jak tak to babka zdziwko będzie miała

ola: dokładnie, muszę się tego nauczyć na koło

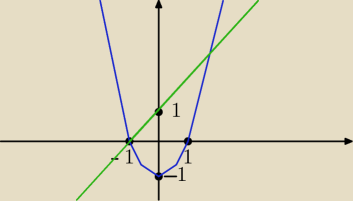
Kejt: proszę

bart: podoba mi sie to

SzymeQ: ale całki, chodzisz na studia czy średnia szkoła, bo to można w graficzny sposób zrobić. Bez użycia całek

Grześ: dzięki za rysunek Kejt, chociaż drobna pomoc z Twojej strony

Grześ: SzymeQ, tej całki raczej graficznie nie policzysz, bo masz już krzywą drugiego stopnia

Kejt: "chociaż" pff.. planuję nauczyć się całek..w tym roku jeszcze..zacznę od rysunków

bart: @SzymeQ koło−kolokwium, wiec to studia ale pokaz jak inaczej zrobic

SzymeQ: rzeczywiście nie popatrzyłem

Grześ: ale chodzi mi o to, że ktoś pofatygował się rysunek zrobić, o to Kejt chodziło mi Ja Ci szczerze dziękuje

Kejt: dobra, dobra.. teraz się nie wykręcaj. No dobrze.. wierzę Ci.

ola: a ja dziękuję Wam !

Grześ: hehe.. chociaż teraz zgoda panuje Pamiętam jak parę miesięcy temu walczylismy o zadania... ahhh...

Grześ: Nadal ten sam Grześ, nie wiem czy pamiętasz

Kejt: nie walczyliśmy.. to Ty mi je zabierałeś. nie zapomnę Ci tego!

ola: to mam jeszcze jedno jak chcecie

Grześ: No Kejti... Wybacz mi dawne urazy

ola: Oblicz pole powierzchni obszaru zawartego pomiędzy y=x²−1 oraz y=−x+1. Narysuj ten obszar.

Grześ: Czy nie potrafisz znaleźć analogię To ciągle to samo, czyli liczysz przecięcia etc.

bart: @Grześ no jak? przeciez minus sie pojawil

Kejt: no dobrze.. skoro tak ładnie prosisz. Wybaczam. Ja nie mam pojęcia o co w tym chodzi, więc mogę co najwyżej rysunek zrobić

Grześ: O co chodzi bart O jaki minus Między górną a dolną granicą całkowania stawia się minus W tamtym przypadku w innym wątku jedna z granic była równa 0, więc nie pisałem −0

bart: no ze y=−x+1 teraz jest bo bylo y=x+1..

Grześ: to jest inny przykład

Grześ: dasz radę Ola Zrób porządny rysunek, znajdź punkty przecięcia, oznacz funkcję wyższą etc. Taki sam schemacik

bart: wiem..

Kejt: w przedostatniej linijce przy 3. się gubię

Grześ: nie rozumiem... w czym problem Kejti cos wyjaśnić

Kejt: skądś Ty te ułamki wytrzasnął..

Grześ:

	1
aaa... w pamięci liczyłem −23*		etc.
	3

Podstawiasz pod górną granicę x=2 i odejmujesz granicę dla x=−1

Grześ: a przed podstawieniem wartości ułamki wytrzasnąłem z praktycznie podstawowej całki nieozaczonej Oto wzorek:

	1
∫ xa dx =		xa+1+C
	a

Grześ: nieoznaczonej*

Kejt:

	1
tak, to dalej rozumiem.. ale skąd wziąłeś tą −		na przykład.. w dodatku z wyższą potęgą
	3

niż była przy 'x'..

Grześ: kurcze, tam miałbyć tak:

	1
∫ xa dx =		xa+1+c... przemęczenie już
	a+1

Kejt: ładne literki.. chyba pójdę już spać

Grześ: zobacz na wzór, całkując −x², podstaw pod wzór: a=2 a minus zostaw przed wyrażeniem

Kejt: aa..taki bajer

Grześ: ale takie całki już w pamięci się wykonuje, a wzór pokazałem dla wyjaśnienia To są praktycznie najprostsze całki...

Kejt: dobra.. a czemu x³? to przez ten mianownik?

Grześ: To w takim razie dobranoc... jak coś, jakbyś chciała Kejti, to mogę jutro pomordować z Tobą całki Kolorowych snów życzę... bez całek

Kejt: cofam to.. nie zauważyłam we wzorze..

Kejt: łaa..byłoby cudnie, gdyby Ci się chciało. W sumie do matury się nie uczysz.. heh. Jako jeden z niewielu tutaj.. dobranoc Grzesiu