;d pafcio: jak mam cos wykazac to co ja biedny mam poczac w takiej sytuacji for example: wykaz ze jezeli k>0 to rownanie x² +k(x−1)=0

kaa: to co rownanie?

pafcio: ahaaaa hahahaa c.d ma dwa pierwiastki

Suiseiseki: to na pewno jest cała treść?

pafcio: jak mam cos wykazac to co ja biedny mam poczac w takiej sytuacji for example: wykaz ze jezeli k>0 to rownanie x2 +k(x−1)=0 ma dwa pierwiastki no juz jest cala tresc

Suiseiseki: bierzesz jako a współczynnik przy x², jako B, k, i jako C −k, szkuasz z tego delty, i sprawdzasz, czy jest wiekrza od 0.

kaa: a wiec; x²+ kx −k=0 Licze delte aby sprawdzic ile ma pierwistkow. Jezeli Δ>0 to dwa Jezeli Δ<0 to zero jezeli Δ=0 to jeden podwojny. Δ=k² +4 a to zawsze wieksze od zera wiec rownanie to ma dwa pierwiastki.

Suiseiseki: Δ=k² +4k chyba tak powinno byc?

pafcio: a to takie micyje

pafcio: tak tak masz racje

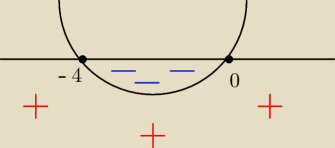
Kejt: x²+k(x−1)=0 x² + kx −k =0 równanie ma dwa pierwiastki jeśli Δ≥0 więc: k²−4*(−k)≥0 k²+4k≥0 k(k+4)≥0 k=0 v k=−4 k∊(−∞;−4>∪<0;+∞) dla tego przedziału to równanie ma dwa pierwiastki dokładamy warunek, że k>0 i eliminujemy jeden przedział. Wychodzi: k∊(0;+∞) czyli jest to zgodne z prawdą..

ewela: Wskaz,ze jezeli k>0 to rownanie x⁺k(x−1)=0 ma dwa miejsca zerowe

Janek191: Przepisz porządnie równanie