s
Adam: UDOWODNIJ ZE − mam taki maly problem
Dany jest trójka
t ABC. Na boku |BC| tego trójkata wybrano taki punkt D,
ze kat DAC jest równy katowi CBA. Odcinek |AE| to dwusieczna kata
BAD. Udowodnij, ze bok |AC| jest równy bokowi |CE|.
dzieki za wytlumaczenie
2 maj 18:24
Adam: 
2 maj 18:39
Adam:
2 maj 20:13
Adam: odswiezam
2 maj 20:34
Adam:
2 maj 20:45
uhu: Narysuj to
2 maj 20:47
Adam:
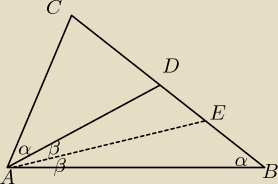
2 maj 20:53
Adam: i jak?
2 maj 21:03
Adam:
2 maj 21:11
uhu: No czekaj, muszę pomyśleć bo nie mam pomysłu ^^
2 maj 21:15
uhu:
2 maj 21:20
Adam: nie che Ci nic mowic, ale to jest podstawa
2 maj 21:25
2 maj 21:25
uhu: No ale wiesz "wykaż" ^^ napisałem ci mój sposób który w sumie jest trochę dziwny i nie wiem czy
poprawny ale w tej chwili mi nic innego do głowy nie przychodzi, już mózg wysiada
2 maj 21:28
Adam: odswiezam
3 maj 00:31
Adam:
3 maj 01:10
Eta:
Uwzględniam
Adam ...Twój rysunek:
|<CAE|= α + β to |<AEB|= 180
o −(α+β) => |<AEC|= α+β
i | <EAC|= α+β
co oznacza że ΔAEC jest równoramienny o ramionach AC i CE
zatem |AC| = |CE|
c.n.u
3 maj 01:33
Suiseiseki: bump, tez mordowałam sie nad tym zadaniem godzinę.
Miałam pomysł zeby jakos wykorzystac podobienstwo trójkątów |ABC| i |ACD|, ale nie mam juz sił
na jego realizaje.
3 maj 01:37
;): Dla
Ety 
...
3 maj 01:47
wolfy: heh zrobilem podobnie jak Eta, lecz najpierw wypisalem wszystkie katy w trojkacie, a pozniej
uroilem sobie ze ΔAEC jest rownolegly lecz inne ramiona sa rowne wiec nie dowiodlem tego xD
ale ze mnie idiota...
3 maj 02:18
Eta:
3 maj 03:06