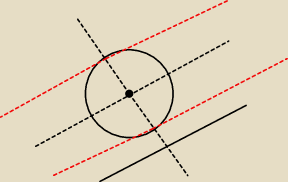
Geometria analityczna Jordan: Mam wyznaczyć równania prostych stycznych do okręgu o jakimś równaniu i równoległych do prostej np. y = 2x + 2. Tradycyjnie to robił bym w ten sposób: Szukam współrzędnych środka okręgu znajduje równanie prostej równoległej do y = 2x + 2 przechodzącej przez ten środek. Potem równanie prostej prostopadłej do otrzymanego wcześniej równania przechodzącej przez środek. W ten sposób znajduje współrzedne dwóch punktów stycznych do okręgu i dopiero wtedy piszę równanie prostej równoległej do y = 2x + 2 przechodzącej właśnie przez te dwa punkty. Ehhh Da się to zrobić jakoś szybciej?

Oluś: Fakt faktem sporo liczenia... ale chyba nie da sie szybciej

adrian: jeżeli masz podany promień i współrzędne środka (lub jeżeli da się je obliczyć): równanie prostej równoległej : y = 2x + c równanie okręgu: (x−a)² + (y−b)²) = r² masz układ równań, do drugiego wstawiasz y z pierwszego i doprowadzasz do postaci równania kwadratowego potem oblicz Δ i załóż Δ=0, z tego założenia wyjdzie ci dwa c

adrian: tzn powinno wyjść dwa c bo tam powstaje drugie równanie kw. z niewiadomą c, chyba że to jest szczególny przypadek i c² się zredukuje (nie wiem nie liczyłem)

Jordan: w sumie racja dzięki

sasiad: dajesz s*y