równanie Joanna: Wyznacz współrzędne punktu P leżącego na wykresie funkcji y = 7x − x² − 15 , dla którego suma odległości od osi układu współrzędnych jest najmniejsza. Jak to rozwiązać?

uhu: Ja bym to zrobił tak, wyznaczasz odległość pkt (x,−x²+7x−15) od osi OX i to samo od osi OY dalej ich suma będzie najmniejsza gdy one będą miały najmniejsze wartości więc liczniki "d=" muszą mieć najmniejsze wartości. Spróbuj,

Oluś: szybciej, że po prostu odległość od osi Ox to IyI a odległość od osi Oy to IxI Wtedy tylko tworzysz funkcję s= IxI+IyI= IxI+I−x²+7x−15I i szukasz dla jakiego x osiąga ona minimum

Joanna: Mam to tego rozwiązanie (z zadania.info), tak samo jak Oluś, ale nie rozumiem czemu tam zmienia się z S = |x| + |y| = |x| − y

Joanna: Może ktoś wytłumaczyć?

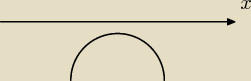
Oluś: −x²+7x−15 ta funkcja nie ma miejsc zerowych a jej ramiona są skierowane do dołu więc wygląda to tak jak na rysunku czyli jest zawsze mniejsza od zera Dlatego pomijajac wartość bezwzględną z y robi się −y

Oluś: Jak jeszcze coś wyjaśnić to pisz

Joanna: A jakby nie była cała? To jak wtedy/?

Oluś: Nie bardzo rozumiem

Joanna: Jak delta nie była na minusie

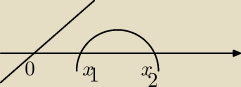
Oluś: dla delty większej od zera będziesz miała taki rysunek gdzie x₁ i x₂ to pierwiastki i wtedy po prostu musisz rozpatrzyć więcej przedziałów

uhu: Mógłby ktoś podać jaka jest odpowiedź do tego zad ? Próbuje innym sposobem i chce wiedzieć czy wychodzi

Oluś: Dokładniej dla x∊ (−∞, 0) S = |x| + |y| = −x − y dla x∊ <0, x₁) ∪ <x₂, +∞) S = |x| + |y| = x − y dla x∊ <x₁,x₂) S = |x| + |y| = x + y

Oluś: Mi wyszło P (3,−3)

uhu: no p mi się zgadza ale to pewnie przypadek, q mi wyszło 6 ^^ ale ten mój sposób to taki ruski więc go jeszcze dopracuje