Twierdzenie sinusów i cosinusów. Sylwia: 1) Wykaż, że w dowolnym równoległoboku suma kwadratów długości przekątnych jest równa podwojonej sumie kwadratów długości boków. 2) Oblicz cosinus kąta ostrego pomiędzy środkowymi trójkąta prostokątnego równoramiennego, poprowadzonymi z wierzchołków kątów ostrych. 3) Długości boków trójkąta są trzema kolejnymi wyrazami ciągu arytmetycznego. Obwód trójkąta

	1
wynosi 21cm, a cosinus największego kąta w tym trójkącie jest równy −		. Wyznacz
	10

długości boków tego trójkąta.

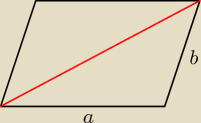
uhu: 1. Dwa kolejne kąty w równoległoboku mają razem 180 2. Zastosuj 2x twierdzenie cosinusów

kamis: x,y − długości boków, x,y ∊ R⁺ e,f − przekątne e² = x² + y² − 2xycosα f² = x² + y² − 2xycos(180 − α) = x² + y² + 2xycosα e² + f² = x² + y² − 2xycosα + x² + y² + 2xycosα = 2x² + 2y² = 2(x² + y²)

Sylwia: Podbijam

elk: chyba się znaki nie zgadzają