awdawdawda KOLEGA: Równania kwadratowe Chciałbym, żebyście sprawdzili mi kilka równań kwadratowych, które właśnie rozwiązuję. Mam nadzieję, że mogę liczyć na waszą pomoc. x²−|x|−12=0 WYNIK x=−4 lub x=4 x²+x+|x−2|=7 WYNIK x= −√5 lub x= −1 + √10 Działania będę konsekwentnie dodawał. Nie wiem z jakiej książki są te zadania, więc nie mam możliwości sprawdzić odpowiedzi. Pod zadaniami jest jedynie "A gdyby sprawdzian był teraz ?" i kolejne przykłady. Jeżeli ktoś z was ma możliwość podesłania mi wyników do tych zadań i wie która jest to książka, byłbym wdzięczny.

KOLEGA: 2x²+3|x|−9=0 WYNIK x=³₂ lub x=−³₂

KOLEGA: (|x|−3) (2−|x|)=0 WYNIK x∊∅ Wymnożyłem wszystko przez siebie i dopiero obliczałem deltę, ale powinna być jakaś krótsza droga. Ma ktoś pomysł ?

KOLEGA: Nikt nie potrafi mi pomóc ?

;): Dla x ≥ 0 (x − 3)(2 − x) = 0 Dwa rozwiązania x = 3 i x = 2 dla x < 0 −(x + 3)(x + 2) = 0 dwa rozwiązania x = −3 i x = −2 Wiec są 4 rozwiązania x ∊ {−3,−2,2,3}

KOLEGA: ale przecież jeśli wymnożymy i obliczymy delte to wychodzi ona poniżej zera.

;): Jak Ci wyjdzie Δ < 0 pokaż swoje obliczenia

KOLEGA: najpierw wszystko wymnażam przez siebie wychodzi: 2|x|− |x|² −6 +3|x|=0 5|x|− x² −6 =0 −x²+5|x|−6=0 Później przypadki z pierwszego (R+ U {0}) −x² +5x−6=0 Δ25−25 =1 x1= 5−1=−2 −> nie należy do dziedziny x2= −3 −> nie należy do dziedziny z drugiego przypadku x3=2 −> nie należy do dziedziny x4=3 −> nie należy do dziedziny

;): Masz postać iloczynową to po co utrudniać sobie życie i wszystko wymnażać? W dodatku jeżeli już chcesz wszystko przez wszystko wymnażać to sobie sprawdzaj dwa razy x ≥ 0 −x² + 5x − 6 = 0 Δ = 25 − 24 ! błąd nie wiem z czego on wynikał √Δ = 1

	−5 − 1
x1 =
	−2

x₁ = 3 x₂ = 2

KOLEGA: W obliczaniu pierwiastka zamiast −5 pisałem 5... a w delcie chyba nie ma błędu. Jeżeli zamieniłem 5 na −5 to wyniki są dobre. Czy mógłbyś sprawdzić poprzednie równania? Mam jeszcze sporo pracy dzisiaj..

KOLEGA: |x² +x −12|−6≥0 x∊<−2;3> Dziwne wyniki mi wychodziły w pierwzym przypadku. Mógłby ktoś to sprawdzić ?

KOLEGA: Jest to chyba Matematyka 1 Poznać zrozumieć Podręcznik. Zakres podstawowy i rozszerzony. Liceum, technikum albo zbiór. Jeżeli ma ktoś tę książkę w domu, prosiłbym o ze skanowanie samych wyników do zadań które podałem. Zadanie 1,2,3 i "a gdyby spradzian był teraz".

;): 1^o x∊(−∞,−4>∪<3,∞) x² + x − 18 ≥ 0 2^o x∊(−4,3) x² + x − 6 ≤ 0 Rozwiązać i tyle

KOLEGA: Mógłbyś napisać jak to obloczyłeś bo mi wyszły inne liczby. a Δ w pierwszym przpadku wychodzi dziwna. Nie będzie mnie teraz 20 min ale mam nadzieje ze ktos sprawdzi te równania które napisałem wyżej bo bez nich nie rusze dalej.

;): Ja sam nie wiem czy jeszcze będę

KOLEGA: Jestem. Dalej proszę o pomoc w sprawdzeniu równań które na górze napisałem. Mam problem również z tym ostatnim. Pomocy!

asd: Napisz raz jeszcze tresc zadania do ktorego potrzebujesz pomocy to zrobie

KOLEGA: Chciałbym, żebyście sprawdzili mi kilka równań kwadratowych, które właśnie rozwiązuję. Mam nadzieję, że mogę liczyć na waszą pomoc. x²−|x|−12=0 WYNIK x=−4 lub x=4 x²+x+|x−2|=7 WYNIK x= −√5 lub x= −1 + √10 2x²+3|x|−9=0 WYNIK x=³₂ lub x=−³₂ |x² +x −12|−6≥ tutaj prosiłbym o policzenie kiedy to co jest pod wart. bezwg. jest nieujemne, potem sprobuje sam.

;): W ostatnim pisałem dla x∊(−∞,−4>∪<3,∞) jest dodatnie x² + x − 12 a dla x∊(−4,3) jest ujemne −x² − x + 12

;): Wszystko dobrze tylko teraz zrób to ostatnie

KOLEGA: więc miałeś racje. Tylko teraz pierwiastki wychodza mi nie równie. x1= ~ − 4,7 ∊D x2= ~3,8 ∊D z 2 przypadku x1=3 −> nie należy do D x2= −2 −> należy do dziedziny.

;): Ale z czym miałem racje?

KOLEGA: źle liczyłem kiedy jest nieujemne. Dobrze mi wyszło ? Co mam zrobić jeżeli wychodzi mi tylko x1 w jedym przypadku, a 2 w drugim przypadku.

;): Które zadanie napisz bo nie wiem o które chodzi

KOLEGA: chodzi mi o ostatni przykład |x² +x −12|−6≥0 bo reszte sprawdziłeś i są dobrze, tak ?

kook: x2−|x|−12=0 WYNIK x=−4 lub x=4 W tym mi taki sam wynik wyszedł jak tobie.

kook: Natomiast w drugim mam x₁ = −√5 a x₂ = 1+ √10

KOLEGA: Myślałem, że jeśli sam rozwiąże równania i będę prosił tylko o sprawdzenie, to chętnych będzie masa.

;): x = −1 + √10 będzie

;): Więc dobrze ma KOLEGA

;): |x² + x −12| − 6 ≥ 0 i co rozwiązałeś już to?

KOLEGA: napisałem wyżej x1= ~ − 4,7 ∊D x2= ~3,8 ∊D z 2 przypadku x1=3 −> nie należy do D x2= −2 −> należy do dziedziny. Czy dobrze są policzone te pierwiastki ?

;): Tylko że Ty masz tam nierówność

;): Z pierwszego będziesz miał

	1 + √73		−1 + √73
x∊(−∞,−		)∪<		,∞)
	2		2

z drugiego x₁ = 2 x₂ = −3 x∊<−3,2>

KOLEGA: więc z pierwszego przypadku x∊(−∞;~4,7> U <~3,8;∞) z drugiego przypadku mam tylko x2= −2 bo x1 nie należy do dziedziny z drugiego x∊{−2}

;): x ₁ = 2 x₂ = −3! źle liczysz miejsca zerowe

KOLEGA: z drugiego Δ=25 x1= −1−5/:−2= 3 x2= −1+5/−2= −2

;): x² + x − 6 ≤ 0 Tracę cierpliwość powoli!

;): Na oko widać że miejscami zerowymi bez liczenia jest 2 i −3

KOLEGA: to mam już za sobą. Mam nadzieje ze masz jeszcze czas i cierpliwość żeby mi pomóc. Dzisiaj chce zrobić same przykłady z f kw, dopiero jutro wezmę się za parametry...

;): To jak będę umiał pomóc to pomogę tylko że ja za chwile też pójdę uczyć się polskiego

KOLEGA: |x−4|+|x|=x²−1 Jak zrobić takie działanie ?

kaśka: x2−|x|−12=0 możecie mi to rozpisać:(

;): 1^o x∊(−∞,0) −x + 4 − x = x² − 1 2^o x∊<0,4) −x + 4 + x = x² − 1 3^o x∊<4,∞) x − 4 + x = x² − 1 I sprawdzaj wyniki z 1^o 2^o 3^o czy spełniają

;): Na górze jest rozpisane więc zerknij

kaśka: : W ostatnim pisałem dla x∊(−∞,−4>∪<3,∞) jest dodatnie x2 + x − 12 a dla x∊(−4,3) jest ujemne −x2 − x + 12 o tym mówisz? ja rozbiłam to na (x²−x−12=0) i za pomocą delty wyszło mi 4 i −3.. 4 się zgadza, ale to −3 przecież nie pasuje. A jak dojść do tego, żeby wyszło −4 z obliczeń?

kaśka: Jak rozbić ten moduł na dwa etapy? i jak wykluczyć to zbędne −3?

;): x² − |x| − 12 = 0 Jeżeli o to Ci chodzi to masz dwa warunki dla x ≥ 0 x² − x − 12 = 0 z tego wychodzi −3 i 4 czyli 4 spełnia bo x ≥ 0 i dla x < 0 x² + x − 12 = 0 z tego wychodzi −4 i 3 czyli −4 spełnia bo x < 0

kaśka: Dokładnie o to mi chodziło Nie mogę sobie wybaczyć, że zapomniałam o tym. Wielkie dzięki

;): Proszę bardzo

KOLEGA: |x²−1| + |x²+1|=2 Jak zrobić to ?

;): |x² − 1| + x² + 1 = 2 dla x ∊ (−∞,−1>∪<1,∞) x² − 1 + x² + 1 = 2 dla x ∊ (−1,1) −x² + 1 + x² + 1 = 2 → tutaj coś zauważyć powinieneś

KOLEGA: Dla każdej liczby rzeczywistej wynik będzie dodatni w x²+1.

KOLEGA: a działanie |x²+|x|−12|≤0

;): Tak ale w drugim rozwiązaniu mi chodzi o to −x² + 1 + x² + 1 = 2

KOLEGA: tzn o co?

;): x² + |x| − 12 ≤ 0 ⋀ x² + |x| − 12 ≥ 0 dla x ≥ 0 dla x < 0 x² + x − 12 ≤ 0 ⋀ x² − x − 12 ≥ 0

;): −x² + 1 + x² + 1 = 2 że powinieneś coś widzieć w tym równaniu

KOLEGA: równanie tożsamościowe ?

;): Tak i dlatego tam będą spełniały wszystkie liczby należące do zbioru x∊(−1,1)

KOLEGA: Wielkie dzięki, jeżeli znajde jeszcze dzisiaj troche czasu to będę się na tym męczył i mam nadzieję, że sprawdzisz moje obliczenia.

Misia ;) : Wyznacz wszystkie wartisci parametru m, dla których równanie x² +2mx − 2m +3=0 dwa różne pierwiastki należące do przedziału (−2,0)

KOLEGA: KOLEJNE RÓWNANIE |x−4|+|x|=x²−1 1. Przypadek x∊(−∞;0) x1= −1+√6 nie należy do Df x2= −1−√6 należy do Df 2, Przypadek x∊<0;4) x1= √5 należy do Df x2= −√5 nie należy do Df 3. Przypadek Δ<0 więc x∊∅ Mógłby ktoś to sprawdzić i ewentualnie powiedzieć gdzie jest źle i co ?

KOLEGA: pomoże ktoś ?

M4ciek: Czemu 3 przypadek to : Δ < 0 , a nie x ∊ <4,+∞)

KOLEGA: oczywiście przypadek to <4;∞), a w dalszych obliczeniach Δ jest mniejsza od 0 więc nie ma pierwiasktów. Zapomniałem tego napisać.

M4ciek: No i podaj odpowiedź bo by się przydała..

KOLEGA: Czyli podsumowując, mam nadzieję,że o to ci chodzi, w przedziale (−∞;0) x= −1− √6; w przedziale <0;4) x=√5; w przedziale <4;∞) równanie nie ma rozwiązań.

KOLEGA: Prosiłbym o sprawdzenie tamtego, bo już następne czekają w kolejce .

;): Chwilka za chwile sprawdzę

;): Wszystko w porządku czyli x∊{−1 − √6 , √5}

KOLEGA: ciebie mi tu brakowało zaraz napisze następne.

KOLEGA: |x−1| + |x+1|=x² 1. x∊(−∞;−1) x=0 −> nie należy do Df x=−2 −> należy do Df 2. x∊<−1;1) x= √2 −> nie należy do Df x= −√2 −> nie należy do Df 3. x∊<1;∞) x=0 −> nie należy do Df x=2 −> należy do Df Odp. x∊{−2;2}

;): Zgadza się

KOLEGA: 2|x−5| +x² −2x+3=|3−x| 1. x∊(−∞;3) Δ<0 więc x∊∅ 2. x∊<3;5) Δ<0 więc x∊∅ 3. x∊<5;∞) x1= −1−√41/2 −> nie należy do Df x2= −1+√41/2 −> nie należy do Df Odp. x∊∅

;): W porządku

KOLEGA: |x²−1|+|x²+1|=2 tutaj napiszę co robię krok po kroku, żebyś ewentualnie wskazał braki. sprawdzam kiedy |x²−1| jest większe lub równe 0. Wykresik 1. x∊(−∞;−1>U<1;∞) x²−1+x²=1=2 x=−1 −> x∊Df x=1 −> x∊Df 2. x∊(−1;1) 2=2 równanie tożsamościowe Odp. x∊R. Nie wiem czy umiałbym zrobić równianie gdyby druga wartość bewzględna z kwadratem była inna, ale tym zając bym się chciał ewentualnie poźniej. Najpierw ważniejsze rzeczy.

KOLEGA: Najpierw napisze ci co zrobiłem i ty to sprawdzisz ewentualnie później (może jutro) nowe rzeczy. x²−4|x|+3>0 Odp. x∊(−∞;0) U (4;∞) Następne x²−2x−3|x+1|−2<0 x∊<5−3√5/2 ; 5+3√5/2}

Jack: lepiej to popraw kolego... (|x²−1|+|x²+1|=2 ) Widać, że np. dla x=10 wynik będzie znacznie większy niż 2...

;): |x² − 1| + |x² + 1| = 2 2^o dla x∊(−1,1) zgadzam się że to jest równanie tożsamościowe ale masz dziedzinę z góry nałożoną więc 2^o x będzie należał do przedziału x∊(−1,1) Końcowy wynik to x∊<−1,1>

;): Witam Jack

KOLEGA: oczywiście. Następne przykłady napisałem wyżej.

Jack: Witaj

;): Ale masz tylko algebraicznie rozwiązywać czy możesz też graficznie?

KOLEGA: polecenie brzmi: Rozwiąż równianie. Ale na lekcji rozwiązywaliśmy takie nierówności algebraicznie.

;): x² − 4|x| + 3 > 0 1^o x ≥ 0 x∊(0,1>∪<3,∞) 2^o x < 0 x∊(−∞,−3>∪<−1,0) x∊(−∞,−3>∪<−1,0)∪(0,1>∪<3,∞)

;): Poszukaj gdzieś błędu u siebie a ja sprawdzę czy na pewno mam dobrze bo mamy w tym inne wyniki

KOLEGA: My na lekcji robiliśmy to chyba troszkę inaczej. Pod wartością bewzględną jest jedynie x. Więc rozpisuje na 2 przypadku x²−4x+3>0 dla x∊R+ U {0} x²+4x+3>0 dla R− Z pierwszego wyliczam Δ, x1,x2 które należa do dziedzine. Wykresik i wychodzi x∊(−∞;0)U(4;∞) Pod wartością jest sam x więc x3 jest przeciwny to x1 a x4 jest przeciwny do x2 x3=4 −> nie należy do dziedziny x4=−1 −> należy do Df równanie ma być większe od 0 więc miejsce zerowe x4 nie przydaje się.

;): Znowu liczyć nie umiesz miejsc zerowych chyba

;): Graficznie by się to robiło w parę sekund tą nierówność

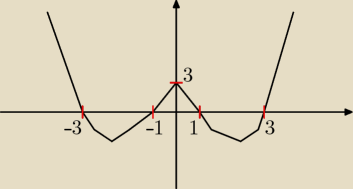
;): Widać gdzie jest nad osią OX

KOLEGA: mam to

;): Co masz to?

KOLEGA: Mógłbyś następne sprawdzić ? x²−2x−3|x+1|−2<0 x∊<5−3√5/2 ; 5+3√5/2>

KOLEGA: znalazłem błąd w poprzednim i poprawiłem− to miałem na myśli.

;): Również mi tyle samo wyszło

KOLEGA: x²+4x+2|x−1|+3>0 x∊∅

;): x2 − 4|x| + 3 > 0 Źle spojrzałem ma być ≥ 0 więc odpowiedź będzie x∊(−∞,−3)∪(−1,1)∪(3,∞)

;): Ech > 0 tak jest a ja zrobiłem ≥ 0

KOLEGA: wynik w tym równianiu do którego wróciłeś x∊(−∞,−3)∪(−1,1)∪(3,∞)

;): x² + 4x + 2|x−1| + 3 > 0 Mi wyszło x∊R

;): Wiem bo poprawiłem właśnie ubzdurałem sobie że jest ≥ 0 a było > 0

KOLEGA: 2 przypadki x∊<1;∞) x²+4x+2x−2+3 Δ=32 x1= −3−√8 −> nie należy do dziedziny x2= −3+√8 −> nie należy do dziedziny 2 przypadek x∊(−∞;1) x²+4x−2x+3>0 x²+2x+5 Δ<0 x∊∅

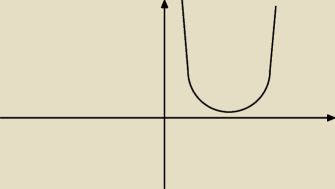
;): Parabola leży w całości nad osią OX mamy nierówność > 0 więc x∊R

;): Rozumiesz skąd się to wzięło?

KOLEGA: Nie wiem za bardzo jak rysujesz te nierówności, a przede wszystkim nie wiem gdzie mam błąd w tych nieszczęsnych obliczeniach .

;): x² + x + 6 > 0 Rozwiąż tą nierówność podaj zbiór x które spełniają tą nierówność

KOLEGA: Czy my mówimy o tym samym równaniu ? Ja mam na myśli x² + 4x + 2|x−1| + 3 > 0 a tam x²+x+6>0 nigdzie nie wychodzi.

;): x² + x + 6 > 0 Chce żebyś je rozwiązał i podał zbiór x które należą do tej nierówności

;): Wtedy będzie Ci łatwiej zrozumieć tamtą nierówność

KOLEGA: x∊(−∞;−3)U(2;∞)

;): Policz jeszcze raz Δ

KOLEGA: Ja już wiem o co ci chodzi, tylko że Δ jest mniejsza od 3 w tym drugim przedziale, a w pierwszym jest większa i ma pierwiastki, które nie należa do dziedziny i nie moge sobie tego zobrazować.

;): Ale źle sobie to tłumaczysz ma pierwiastki które nie należą tak ale to jest nierówność a nie równanie

;): Dam Ci przykład x² − x − 12 < 0 i D_f jest x∊(−1,∞) Rozwiąż to uwzględniając D_f

KOLEGA: jest za późno chyba żebym to teraz zrozumiał. Napisze ci inne równanie żebyś sprawdził a jak zdąże to i coś nowego, czego kompletnie nie umeim rozwiązać.

KOLEGA: x²+3|x|−4≥0 z jednego przypadku x2=1 −> należy do Df a x1 nie z 2 przypadku x4 nie należy do Df, a x4=−1 należy. Co mam w tym przypadku zrobić ? x∊(−∞;−4>U<1;∞)

;): To jak chcesz A do której klasy chodzisz liceum?

;): Jest to nierówność więc zapisuję najpierw dla x ≥ 0 x² + 3x − 4 ≥ 0 x∊(−∞,−4>∪<1,∞) ⋀ x ≥ 0 ⇒ x∊<1,∞) dla x < 0 x² − 3x − 4 ≥ 0 x∊(−∞,−1>∪<4,∞) ⋀ x < 0 ⇒ x∊(−∞,−1> ostatecznie x∊(−∞,−1>∪<1,∞)

KOLEGA: 1

Obóz Koncentracyjny: Ładnie ci to pan ; ) tłumaczy

;):

;): I jak rozumiesz już to?

KOLEGA: Jest to pani ,a problem leży w tym, że nie byłem przez ostatni tydzień w szkole i zaległości się nagromadziły. Nic więcej dzisiaj nie zrozumiem, oczy same mi się zamykają. Dziękuję za pomoc i ,prawdopodobnie, do zobaczenia jutro.

Obóz Koncentracyjny: ; ) z trygonometrii Pani jest równie dobra ?

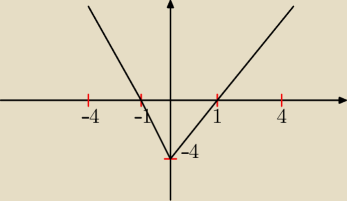
;): Masz taką właśnie funkcję czyli nad osią OX będzie (∞,−1><1,∞) domknięty bo nierówność ostra

;): Kto ja pani? Jestem płci męskiej

;): Ojj nie wiem czy będę jutro bo matura w środę

;): Zależy co by było z tej trygonometrii

KOLEGA: w tym przykładzie to źle dobrałem dziedzinę, dlatego miałem złe wyniki. Czyli: jeśli np. (tak jak tutaj) z x1,x2,x3,x4 do dziedziny należą jedynie x2 i x4, to moge je zaznaczyć na osi, i od nich napisać kiedy x∊, żeby było >/< od 0?

Obóz Koncentracyjny:

	π		π		1
to z trygonometrii sin(x+		)sin(x−		)=
	6		6		2

;): Najpierw zapisujesz dziedzinę x² + 3|x| − 4 ≥ 0 1^o x ≥ 0 Później rozwiązujesz nierówność wychodzi x∊(−∞,−4>∪<1,∞) i teraz sprawdzasz wyniki z dziedziną (−∞,−4> to nam nie siedzi w dziedzinie więc odrzucamy <1,∞) leży nam w dziedzinie bo x ≥ 0 bierzemy z tego cześć wspólną i mamy x∊<1,∞) 2^o identycznie robisz

KOLEGA: No dobra. Chyba rozumiem. Wracając do wczesniejszego przykładu wychodziło, że Δ<0 i a>0 więc wykres nad osią x − zgadzam się. Ale w innym przypadku Δbyła >0, więc jej część leżała pod osią x i miała pierwiastki, które nie należały do Df. Masz pomysł jak mi to wytłumaczyć ?

;): Już robię to zadanko chwilka

Eta: ....... dla "dwukropka"

;):

	√3		1		√3		1		1
(		sinx +		cosx)(		sinx −		cosx) =
	2		2		2		2		2

3		1		1
	sinx −		cos2x =		/ *4
4		4		2

3sin²x + sin²x = 3

	3
sin2x =
	4

	√3		√3
sinx =		⋁ sinx = −
	2		2

Dokończ

;): Dla Ety

;): Jeżeli mamy równanie i pierwiastki nie należą do dziedziny to je odrzucamy natomiast mając nierówność sprawdzamy gdzie one się znajdują i badamy czy nierówność leży w naszej dziedzinie

Obóz Koncentracyjny: Wyjaśnił byś mi tylko pierwszą linijkę ?

;): Dam Ci przykład x² + x + 6 > 0 a > 0 i Δ < 0 więc tą nierówność spełniają wszystkie liczby rzeczywiste x² + x − 12 ≤ 0 i x ≥ 0 rozwiązaniami nierówności jest przedział <−4,3> ale mamy dziedzinę x ≥ 0 bierzemy cześć wspólną i otrzymujemy x∊<0,3> Rozumiesz?

;): sin(x + y) = sinxcosy + sinycosx

;): Obóz Koncentracyjny wzór na sumę

Obóz Koncentracyjny: Usprawiedliwie się tym że jest późno. Tylko że ja nie wiem jak tam ten wzór został zastosowany.

	√3
Przecież tam są tylko sinusy skąd się wzięło		?
	2

KOLEGA: To co napisałeś już jest dla mnie jasne, tylko nie wiem kiedy i w jaki sposób mam rozróżnić czy pierwiastki wpływają na nierówność.

;):

	π		π
sinxcos		+ sin		cosx
	6		6

Wiesz już?

;): Pierwiastki nigdy Ci nie wpływają na rozwiązanie nierówności tylko dziedzina Jeżeli nie masz z góry nałożonej dziedziny to rozwiązujesz zwykła nierówność kwadratową

KOLEGA: Na tamtym przykładzie. x²+4x+2x−2+3>0 dla x<1;∞) Δ=32 x1= −3 −√8 x2= −3+√8 Nie mają części wspólnej, a wynik, jak wiesz, musi być dla x∊R. Dlaczego ?

Obóz Koncentracyjny: a a potem się to skraca ?

;): 1^o x² + 6x + 1 > 0 ⋀ x ≥ 1 Δ = 36 − 4 √Δ = 4√2 x₁ = −3 − 2√2 x₂ = −3 + 2√2 x∊(−∞,−3 − 2√2)∪(−3 + 2√2,∞) ⋀ x ≥ 1 ⇒ x∊<1,∞) 2^o x² + 2x + 5 > 0 ⋀ x < 1 Δ = 1 − 5 Δ < 0 x∊R ⋀ x < 1 ⇒ x∊(−∞,1) Biorąc sumę 1^o i 2^o x∊<1,∞) ⋁ x∊(−∞,1) ⇒ x∊R

;): Ale które się skraca?

;): Jak masz jeszcze jakieś pytania albo ciekawe zadanko to pisz bo za chwilę idę spać

;): Jeżeli nie masz żadnych pytań to idę. Dobranoc

KOLEGA: |x²+|x|−12|≤0 Jak zabrać się za takie równanie ?

KOLEGA:

JaJa: x² +|x|−12≤0 i x² +|x|−12≥0 i do tego po dwa przypadki

jojo: Ja bym to zaczął tak jak źle to niech mnie ktoś poprawi 1.x² + |x| − 12 ≤ 0 i 2.x² + |x| − 12 ≥ 0 1. x² + x − 12 ≤ 0 i x² − x − 12 ≤ 0 2. x² + x − 12 ≥ 0 lub x² − x − 12 ≥ 0

JaJa: oczywiscie z def wartosci bezwzglednej czyli dla x≥0 i dla x<0

;): Ja bym to zrobił bardziej na logikę |x² + |x| − 12| jest zawsze dodatnie a mamy nierówność ostrą ≤ 0 Więc wystarczy rozwiązać równanie x² + |x| −12 = 0 i to będzie naszym rozwiązaniem dla x ≥ 0 x² + x −12 = 0 x₁ = 3 x₄ = −4 ⋀ x ≥ 0 ⇒ x = 3 dla x < 0 x² − x −12 = 0 x₁ = −3 x₂ = 4 ⋀ x < 0 ⇒ x = −3 x∊{−3,3}

;): A jeżeli chcecie tak robić to tak powinno być dla x ≥ 0 dla x < 0 x² + x − 12 ≤ 0 ⋁ x² − x − 12 ≤ 0 ⋀ ⋀ x² + x − 12 ≥ 0 ⋁ x² − x − 12 ≥ 0

jojo: kurde to znowu nie rozumie kiedy jest i a kiedy lub

;): |x − a| ≤ 0 ⇒ x ≤ a ⋀ x ≥ a |x − a| ≥ 0 ⇒ x ≥ a ⋁ x ≤ a

jojo: to dlaczego powyżej zapisałeś tak jak zapisałeś ?

jojo: aha w ten sposób to zrobiłeś dobra już wiem a mogłbyś rozwiązać coś takiego albo chociaż założenia napisać:

	2
|		| < 1
	x−1

jojo: aha w ten sposób to zrobiłeś dobra już wiem a mogłbyś rozwiązać coś takiego albo chociaż założenia napisać:

	2
|		| < 1
	x−1

;): Zapisałem tak jak powinno być więc nie rozumiem Twojego pytania miałem źle zapisać czy jak?

jojo: aha w ten sposób to zrobiłeś dobra już wiem a mogłbyś rozwiązać coś takiego albo chociaż założenia napisać:

	2
|		| < 1
	x−1

jojo: kurde nie wiem co sie stalo mogę cie prosić o rozwiązanie tego ?

;): Dziedzina x ≠ 1

	2
|		| < 1
	x − 1

	2		2
1o		< 1 ⋀ 2o		> −1
	x − 1		x − 1

2 − x + 1
	< 0 /(x − 1)2
x − 1

(−x + 3)(x − 1) < 0 (x − 3)(x − 1) > 0 ⇒ x∊(−∞,1)∪(3,∞) 2^o

2 + x − 1
	> 0
x − 1

x + 1
	> 0 /(x − 1)2
x − 1

(x + 1)(x − 1) > 0 ⇒ x∊(−∞,−1)∪(1,∞) 1^o ∩ 2^o Ostatecznie x∊(−∞,−1)∪(3,∞)

;): Masz odpowiedzi do tego

jojo: o jasny pierun zapomniałem że przy nierównościach mnoży się razy kwadrat mianownika. BTW dzięki za pomoc

;): Na zdrowie. Dobra idę. Może ale może będę później

KOLEGA: Nie rozumiem za bardzo tego równania. Zawsze będę musiał rozpatrywać aż 4 przypadki? Ponadto jeśli podstawie 0, to wynik też będzie dobry.