prawdopodobienstwo miś: A i B są takimi zdarzeniami losowymi zawartymi w Ω, że A ⊂ B oraz P(A) =0,3 I P(B) =0,4. Oblicz P(A∪B). Jak się za to zabrać?

Johny: P(A)+P(B)=0,4+0,3=0,7 jaką masz odpowiedź?

Absolwent: Johny wzór jest taki P(A∪B)= P(A)+P(B)−P(A∩B)

miś: Poprawna odp to 0,4 ale nie wiem jak takie zadania się liczy.

Johny: no

Absolwent: Nie wiem czy dobrze kminę, ale P(A∩B) będzie 0,3?

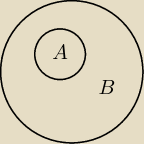
SzymeQ: No ale to na zrozumienie bierzesz, i nie podawajcie błędnych odpowiedzi Jeżeli zdarzenie a zawiera się w b to suma to tylko zdarzenie b, a wy jakieś wzory kij wie co Może na przykładzie lepiej załapiesz: A= 1,2,3 B=1,2,3,4,5 A⊂B czyli suma to zdarzenie B, bo wszystko w B to zbiór A plus jakieś inne co do B wchodzą. Nie umiem tłumaczyć za dobrze ale myślę że skapowałeś. Do tego rysunek John'ego też jest bardzo trafny

SzymeQ: P(A∩B) to 0.3*0.4=0.12 to musisz wziąść na rozum tu nie ma co pisać, ja to od razu walę odpowiedzią No na maturze to raczej coś chociaż słownie napisz ocb

Absolwent: Rozumiem SzymeQ, w mojej poprzednim poście do tego zadania też o to chodziło

Absolwent: Szymeq, ale w takim przypadku to nam się coś z rozwiązaniem nie zgadza

Anna: Gdy A⊂B, to P(AUB) = P(B) = 0,4 (jak to pisał SzymeQ)

SzymeQ: ale co się nie zgadza miś napisał że poprawna odpowiedź to 0.4 pewnie odpowiedzi ma a ja sobie dam głowę uciąć że to na 100% dobrze, nie ma co rozmyślać

miś: A gdy A i B są takimi zdarzeniami losowymi zawartymi w Ω , że A⊂B oraz P(A) = 0,3 i P(B) = 0,7 . Oblicz prawdopodobieństwo różnicy B \ A. czyli skoro skoro A⊂B to: P(B\A)=P(B)−P(A) = 0,5 a poprawna odp to 0,4

SzymeQ: ale 0.7−0.3=0.4, a to jest odpowiedź

SzymeQ: to wszystko łatwo po narysowaniu się utrwala. Jak to sobie zoobrazujesz to jest pestka