Aldo: Jeszcze szybkie pytanko dotyczące okręgów. Mamy całą masę warunków na to czy dwa okręgi są np. rozłączne wewnętrznie, styczne, itd. itp. No i do każdego warunku jest inne kryterium, np. Styczność zewnętrzna : S₁S₂=r₁+r₂ No i wszystko ładnie, ale ja się tych warunków mam na pamięć nauczyć, czy da się je jakoś wyprowadzić ? Bo w tablicach tego nie ma napisanego. Proszę o poradę.

M4ciek: Właśnie dobre pytanie Też poproszę o jakąś podpowiedź

uhu: To jest bardzo proste jeśli sobie rozrysujesz czekaj już ci pokaże

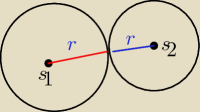
uhu: Widzicie np tu widać że odcinek |S1S2| to suma ich promieni, z resztą przypadków jest tak samo

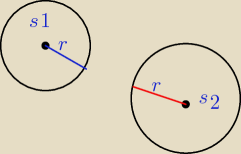
Aldo: No i jak mam dowieźć że są rozłączne ? S₁S₂>r₁+r₂ ?

uhu: no dokładnie skoro odległość między środkami jest większa niż połączone promienie to znaczy że między nimi jest "szpara"

M4ciek: Podsumowując : Okręgi styczne ⇒ IS₁S₂I = r₁ + r₂ Okręgi rozłączne zewnętrznie ⇒ IS₁S₂I > r₁ + r₂ A kiedy są rozłączne wewnętrznie i czy są jeszcze jakieś inne opcje ?

Aldo: ok. A teraz mam podane dwa równania okręgów to co mam z nimi zrobić żeby określić wzajemne położenie ? Nie będę przecież sprawdzać na chybił trafił każdego warunku.

Aldo: M4acku : http://www.interklasa.pl/portal/dokumenty/geom6/geometria6/prezentacja/okrag1b.htm

M4ciek: Wystarczy określić na podstawie promieni no i środków ?

Maryjusz: Jeśli masz dwa równania okręgów to wyznaczasz sobie długości ich promieni oraz liczysz odległość między środkami. Porównujesz te odległości i wiesz już jak są położone względem siebie te okręgi

uhu: Nom masz podane oba promienie i współrzędne obu środków więc obliczasz długość |S1S2| i porównujesz z "r"

Aldo: ok, już sobie poradzę dalej. Dziękuję. Widocznie tak M4ciek