Aldo: Narysuj w układnie współrzędnych zbiór punktów, których współrzędne spełniają nierówność (x+|x|)²+(y+|y|)²≤16. Nie rozumiem jak mam to narysować. Nie widzę tego za bardzo. Możecie to ktoś policzyć "step by step" ? Będę wdzięczny.

marcin: musisz obliczyć 4 równania kolejno dla ujemnej i dodatniej wartości x oraz y. Wyjdą Ci 4 równania okręgu.

Aldo: czyli : (x−x)²+(y−y)²≤16 ? , tylko jaki to ma sens. Nie rozumiem. x²+y²≤4 x²+x²>−4 też nie..

Maryjusz: x≥0 ⋀ y≥0 (x+x)²+(y+y)²≤16 x≥0 ⋀ y<0 (x+x)²+(y−y)²≤16 x<0 ⋀ y≥0 (x−x)²+(y+y)²≤16 x<0 ⋀ y<0 (x−x)²+(y−y)²≤16

bart: 1^o (x−x)²+(y−y)²≤16 2^o (x+x)²+(y+y)²≤16 3⁰ (x+x)²+(y−y)²≤16 4^o (x−x)²+(y+y)²≤16 jedno rownanie okregu bedzie, dwie parabole i jedno nie wiem co, ale wszystko bedzie spelniac rownanie xD

marcin: x²+y²≤4 koło, środek w punkcie (0,0) promień 2 x²≤4 ⇒ x≤2 y²≤4 ⇒ y≤2 (x−x)²+(y−y)²≤16 fakt to chyba nie ma sensu i według mnie trzeba będzie wziąć to wszystko w układ równań

marcin: oj przedmówca dobrze mówi sorki

Maryjusz: ostatnie równanie (x−x)²+(y−y)²≤16 0≤16 ⇒ x,y ∊ R

Rivi: Tylko trzeba dodać, że te cztery równania, każde ma przyporządkowaną do siebie ćwiartkę

1.		(x−x)2+(y−y)2≤16

0≤16 (czyli cała ćwiartka gdzie iksy i igreki są ujemne spełnia tą nierówność, należy do

zbioru)

2. (x+x)²+(y+y)²≤16 (to jest ćwiartka, gdzie iksy i igreki są dodatnie) 4x²+4y²≤16 x²+y²≤4 (czyli ćwiartka koła o środku 0,0, i ćwierćkolu od (0,2) do (2,0), prawy górny róg

układu

3. (x+x)²+(y−y)²≤16 (gdzie iksy dodatnie, ugreki ujemne, czyli prawy dolny róg) 4x²≤16 x²≤4 x∊<−2,2> , iksy tylko dodatnie, więc od (0,2> prawy dolny róg, ze wszystkimi igrekami 4. 4y²≤16 (igreki dodatnie, iksy ujemne, lewy górny róg) y²≤4 y∊<−2,2> igreki dodatnie, więc cała część tej ćwiartki z y∊(0,2> a narysuje! xD

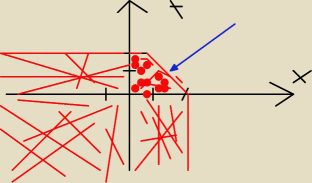
Rivi: to wskazane niebieską strzałką to jest część koła

Aldo: Rivi... Proponuję żebyś jednak pozostał na obliczeniach Ale mimo wszystko bardzo Ci dziękuję. Teraz rozumiem jak zrobić to zadanie

Rivi: fajna zabawa rysowanie tego