awdawdawdawd berek : Dla jakich wartości parametru p funkcja f(x)= ¹_{p{p²+ p−6)x²+(p−2)x+1} w liczniku jest 1, w mianowniku POD PIERWIASTKIEM WSZYSKTO (p²+ p−6)x²+(p−2)x+1

Nie jestem mądry: " Dla jakich wartości parametru p funkcja" ... ale co dalej?

	1
f(x)=
	√(p2+p−6)x2+(p−2)x+1

przem : jest określona dla każdego x∊R

adrian: dwa zał: Δ<0 i a>0 po to żeby funkcja w mianowniku nie miała miejsc zerowych i nie może być ujemna bo jest pierwiastek

Artur: adrian mianownik może być ujemny, nie może być zerem i mieć pierwiastków...

berek : więc jak to ma wyglądać?

adrian: mianownik nie może być ujemny bo to jest pierwiastek kwadratowy, czyli pod pierwiastkiem musi być liczba ≥ 0

bart: ... >0 !

berek : Moglibyście to rozwiązać, bo już sie kompletnie pogubiłem...

Igor: (p2+ p−6)x2+(p−2)x+1>0 obliczasz Δ i te pierwiastki wyrzucasz ze zbioru rozwiązań

berek: Kolejny raz proszę o pełne rozwiązanie tego zadania z wytłumaczeniem swoich ruchów. Z góry dziękuję...

berek : Ma ktoś czas żeby mi pomóc ?

uhu: przepisz to poprawnie z boku masz rożne funkcje typu pierwiastek itp (a nie opisowo) to ci powiem co i jak

berek : w 2 poście "Nie jestem mądry" napisał to poprawnie. Mam nadzieję, że ty mi pomożesz.

uhu: Zobacz mianownik nie może być nigdy zerem ale tu dodatkowo znajduje się pod pierwiastkiem więc jak już ktoś wcześniej pisał nie może być liczbą ujemną więc funkcja (p²+p−6)x²+(p−2)x+1>0 kiedy ta funkcja będzie miała tylko wartości dodatnie ? Dla a>0 i Δ<0. Ale to nie jest koniec bo możemy zauważyć że dla p=2 te założenia też są spełnione i koniec

Igor: (p²+p−6)x²+(p−2)x+1>0 obliczasz pierwszą Δ p²+p−6 Δ=1−4*(−6)=25 √Δ=5

	−1+5
p1=		=2
	2

p₂=−3 wychodzą Ci 2 p podstawiasz: p₁ 2x²+(2−2)x+1>0 2x²+1>0 2x²>−1

	1
x2>−
	2

	1
x1>−√
	2

x₂>√¹₂

Igor: p₂ 3x²−x+1>0 Δ=4−1*3*1=1 nie coś źle robie nie wiem

uhu: Przecież napisałem dokładnie jak trzeba to zrobić ?

Igor: ale dobrze robię ?

uhu: a=2 lub Δ=(p−2)² − 4p²−4p+24=p²−4p+4 − 4p²−4p+24=−3p²−8p+28

	8+20		8−20
√Δp=20 → p=		lub p=
	−6		−6

a>0 czyli p²+p−6>0

uhu: Wiesz już o co chodzi ?

Igor: no mniej więcej jeszcze sobie pogłówkuje. teraz robię tą maturę z zadań.info

uhu: jak coś pisz

:): Jak dla mnie to treśc zadania nie jest pełna : 'Dla jakich wartości parametru p funkcja...' jest... i coś dalej chyba powinno byc.

uhu: Jest w 3 poście dokończone

berek : w 3 poście masz kontynuacje zadania. Przepraszam was, ale mam już dzisiaj wszystkiego dość. Próbuje rozwiązać między innymi to zadanie, ale kompletnie nie mogę pojąć o co w tym chodzi. Gdyby ktoś z was mógł rozwiązać to krok po kroku, żebym mógł to zobaczyć i sobie w głowie ułożyć byłbym bardzo wdzięczny. Tylko ponownie pisze,że nie chodzi mi o jedną linijkę, która nawiązuje do poprzednich, a o nowe, kompletne rozwiązanie, dzięki któremu ,mam nadzieję, zrozumiem zadanie i poprawie choć trochę sobie humor.

uhu: a=2 lub Δ=(p−2)² − 4p²−4p+24=p²−4p+4 − 4p²−4p+24=−3p²−8p+28 −3p²−8p+28<0 √Δp=20 → p=2 lub p= −4²₃ p∊(−∞,−4²₃) u (2,+∞) a>0 czyli p2+p−6>0 √Δ=5 p=2 v p= −3 → p∊(−∞, −3) u (2,+∞) p∊(−∞, −3) u (2,+∞) i p∊(−∞,−4²₃) u (2,+∞) i p=2 →→ p∊(−∞,−4²₃) u <2,+∞)

berek : Dzisiaj już nie mam siły na to, jutro będę próbowął zrozumieć. Tylko na pierwszy rzut oka, dlaczeog p=2 na samym początku ?

uhu: a no właśnie tam ma być p=2 a ja napisałem "a", w takim typie zadań zawsze się sprawdza czy istnieje taki parametr (p,m czy co tam mamy) który daje funkcje stałą, zobacz co sie dziaje dla p=2

Malina: uhu mam pytanie dlaczego a>0? nigdzie nie mamy napisane, że ta funkcja ma byc rosnąca. Zrobiłam tak jak Ty to pierwsza częśc zadania p∊(−∞,−4 2/3) u (2,+∞) i wydawało mi się, że to już koniec zadania.

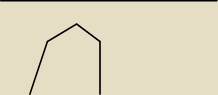
uhu: W połowie postów narysowałem wykres tej funkcji jak musi wyglądać czyli ma cały leżeć nad osią x, gdyby a było <0 wtedy cały leżałby pod osią, narysuj sobie a<<<

Malina: ok dzięki. tylko dalej nie wiem dlaczego po tym jak wyznaczyles przedzialy p zadanie jeszcze nie jest rozwiazane, przeciez jak na poczatku liczyles delte to juz wtedy brales pod uwage dwa rowniania.

uhu: Nie czaje ^^ delta<0 jest warunkiem że funkcja nie jest nigdy zerem natomiast a>0 że dodatkowo nie przyjmuje wartości ujemnych o to ci chodzi ?

Malina: Δ=(p−2)2 − 4p2−4p+24=p2−4p+4 − 4p2−4p+24=−3p2−8p+28 czy rozwiązanie tego równania nie wystarczy jako odpowiedz? Jak mnie nie rozumiesz no to trudno.. Na podstawie raczej tego mi nie dadza Lepiej porozwiazuje cos innego, ale dziekuje za checi

uhu: Poczytaj te posty wcześniejsze a skumasz ocb