Planimetira Ważyh: W trapez prostokątny ABCD wpisano okrąg, przy czym punkt S jest środkiem tego okręgu, a punkt T jest punktem styczności okręgu wpisanego z dłuższym ramieniem . Oblicz pole tego trapezu, jeśli |BT|=8√5 i |SC|=10 .

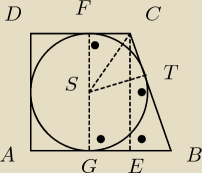
Oluś: IBTI=IBGI=8√5 ICTI=ICFI=x r,x ∊ (0,+∞) IDFI=IAGI=r Z tw. Pitagorasa Δ EBC (2r)²+(8√5−x)²=(8√5+x)² 4r²+320−16√5x+x²=320+16√5x+x² 4r²=32√5x r²=8√5x Z tw. Pitagorasa Δ FCS x²+r²=10² x²+8√5x=100 x²+8√5x−100=0 Δ=320+400=720 √Δ=12√5

	−8√5−12√5
x1=		=−10√5∉(0,+∞)
	2

	−8√5+12√5
x2=		=−2√5∊(0,+∞)
	2

r=√8√5*2√5=√80=4√5

	a+b		2r+x+8√5
P=		*h=		*2r=(2*4√5+2√5+8√5)*4√5=18√5*4√5=360
	2		2

Odp. 360