Tego typu zadania nigdy nie wiem jak zrobić ;/
Absolwent :): Tego typu zadania nigdy nie wiem jak zrobić

. Bardzo proszę o wytłumaczenie krok po kroku jak
do tego się zabrać i od czego zawsze zaczynać. WIELKA PROŚBA

.
Jeśli trzeba rysunki to też proszę o taki rysuneczek

.
Zad.1
Wyznacz równania stycznych do okręgu x
2 + 6x + y
2 − 8y + 21 = 0 równoległych do osi
Oy.
1 maj 15:43
Murzynek: interesuje cie przekrztałcenie równania okręgu do normalnego stanu, czy całokrztałt?
1 maj 15:46
Absolwent :): całokształt niestety

1 maj 15:48
Absolwent :): Tak jak napisałem, od czego zawsze zaczynać w takim zadaniu, na co zwrócić uwagę na starcie itd
1 maj 15:48
Maryjusz: Jeśli proste są równoległe do osi OY to prosta ma postać: y=b
Okrąg: (x+3)
2−9+(y−4)
2−16+21=0
(x+3)
2+(y−4)
2=4
S(−3,4)
r=2
Odległość prostej od środka okręgu musi być równa 2
y−b=0
A=0, B=1, C=−b
|4+b|=2
4+b=2 ⋁ 4+b=−2
b=−2 v b=−6
Proste mają postać: y=−2 ⋁ y=−6
1 maj 15:50
Maryjusz: Ups błąd chyba gdzieś
1 maj 15:52
Murzynek: probujemy doprowadzic X i Y do postaci wzorów skroconego mnożenia.
x2 + 6x + 9 + y2 − 8y + 12 + 4 − 4 = 0
(x + 3)2 + (x − 4)2 = 4
współrzedne sriodka O = ( −3; 4) , R = 2.
Dalszy ciag napisze za chwilę
1 maj 15:53
Maryjusz: |4−b|=2
4−b=2 ⋁ 4−b=−2
b=2 ⋁ b=6
Proste mają postać: y=2 ⋁ y=6
Już dobrze

1 maj 15:54
Murzynek:
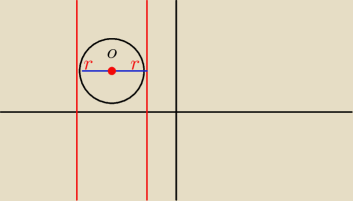
1 maj 15:59
Murzynek: musza byc równolegle od osi OY, więc chyba X = −5, i X = −1
1 maj 16:03
Maryjusz: Aaa haha pomyliły mi się osie OX i OY

Prosta w tym wypadku będzie miała postać y=x
x=−1 ⋁ x=−5
Takie będą te proste

1 maj 16:03
 . Bardzo proszę o wytłumaczenie krok po kroku jak
do tego się zabrać i od czego zawsze zaczynać. WIELKA PROŚBA
. Bardzo proszę o wytłumaczenie krok po kroku jak
do tego się zabrać i od czego zawsze zaczynać. WIELKA PROŚBA  .
Jeśli trzeba rysunki to też proszę o taki rysuneczek
.
Jeśli trzeba rysunki to też proszę o taki rysuneczek  .
Zad.1
Wyznacz równania stycznych do okręgu x2 + 6x + y2 − 8y + 21 = 0 równoległych do osi
Oy.
.
Zad.1
Wyznacz równania stycznych do okręgu x2 + 6x + y2 − 8y + 21 = 0 równoległych do osi
Oy.



 Prosta w tym wypadku będzie miała postać y=x
x=−1 ⋁ x=−5
Takie będą te proste
Prosta w tym wypadku będzie miała postać y=x
x=−1 ⋁ x=−5
Takie będą te proste 