:)
M4ciek:
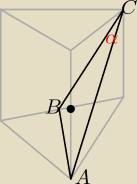
Czy dobrze rozumiem ,że to jest ten kąt

A mianowicie :
W graniastosłupie prawidłowym trójkątnym tg kąta nachylenia przekątnej ściany bocznej i
sąsiedniej ściany bocznej

Czyli policzyć tg α

Dzięki za pomoc

1 maj 15:40
M4ciek:
Podbijam

1 maj 15:53
Rivi: Mi się wydaje, że to jest kąt CAD, gdzie D jest ten róg podstawy w lewym dolnym rogu. Ale ręki
uciąć nie dam
1 maj 15:59
Rivi: I masz przekrój, trójkąt równoramienny, dwie przekątne ściany bocznej i krawędź podstawy... i
da radę tangens wyliczyć mając tą przekątną i krawędź podstawy (lub jakieś cosik, żeby to
wyliczyć)
1 maj 16:02
wolfy:
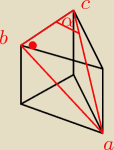
Nie jestem pewien lecz nie powinno być tak?
1 maj 16:02
M4ciek:
Chyba
Wolfy masz rację

1 maj 16:05
Rivi: ale tam chyba nie ma kąta prostego... bo ac=bc, to nie może być
1 maj 16:07
Rivi: tam gdzie prosty też jest α
1 maj 16:07
M4ciek:
Rivi narysuj tak jak Tobie się wydaje

1 maj 16:08
Johny:
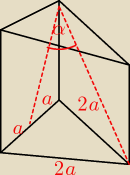
1 maj 16:11
M4ciek:
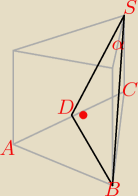
1 maj 16:13
Johny: dokładnie tak, kąt prosty tam jest

1 maj 16:15
Rivi:
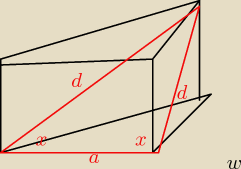
a−krawędź podstawy
d−przekątna ściany bocznej
x−szukany kąt
1 maj 16:17
M4ciek:
A teraz wpiszę całe zadanie :
W graniastosłupie prawidłowym trójkątnym pole powierzchni bocznej równa się sumie pól obu
podstaw.Oblicz tg kąta nachylenia przekątnej ściany bocznej do sąsiedniej ściany bocznej.
1 maj 16:19
Rivi: A masz odp do tangensa? Zaraz oblicze z mojego rysunku i by się spr przydało

1 maj 16:20
M4ciek:
| | a2√3 | |
2 * |
| = 3*a*h / : 3a |
| | 4 | |
Liczyłem dalej i wynik nie pasuje czyli gdzieś mam błąd albo coś jest niezgodne z moim
rysunkiem.

1 maj 16:21
M4ciek:
Rivi , ale Ty masz źle bo Ty narysowałeś :
Kąt nachylenia przekątnej ściany bocznej do przekątnej sąsiedniej ściany

A ma być do ... sąsiedniej ściany bocznej.
1 maj 16:23
Rivi: nie... chodzi mi o "x", to co Ty mówisz to jest kąt na górze, a obliczyć mamy ten na dole. Mi
wyszedł tg=√30 (na szybko, mogłem się machnąć)
1 maj 16:25
M4ciek:
| | 3 | |
No niestety odp. jest tg = |
| |
| | 2 | |
1 maj 16:26
wolfy:
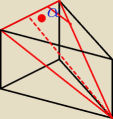
Ehh no faktycznie ale wiem jak to naprawic

wiec to chyba ostateczna wersja

− zadanie z
podstawy chyba?
1 maj 16:27
Rivi: no dobra, mam źle

1 maj 16:27
M4ciek:
Chyba nie z podstawy

1 maj 16:28
Rivi: nie no! no to mam to co Wolfy

czyli też źle

1 maj 16:28
M4ciek:
Chyba musimy poczekać na kogoś mądrzejszego

1 maj 16:29
1 maj 16:37
M4ciek:
A jednak źle policzyłem

Dziękuję
Rivi

1 maj 16:40
nikka: a jaka jest dokładnie treść zadania ?

1 maj 16:40
wolfy: nie rozumiem jednak czemu musi być tak rysunek

1 maj 16:42
wolfy: M4ciek mógłbyś wyjaśnić mi dlaczego tak narysowałeś? Byłbym wdzięczny...
1 maj 16:49
M4ciek:
Wolfy przeczytaj to co wkleił Rivi i myślę ,że Ci się wyjaśni

1 maj 16:58
M4ciek:
Wolfy zaraz Ci wkleje rysunek taki bardziej przyzwoity

1 maj 17:06
M4ciek:
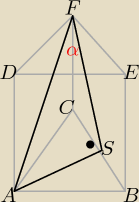
IASI to wysokość w Δ równobocznym , a IFSI można łatwo wyliczyć

1 maj 17:10
 Czy dobrze rozumiem ,że to jest ten kąt
Czy dobrze rozumiem ,że to jest ten kąt  A mianowicie :
W graniastosłupie prawidłowym trójkątnym tg kąta nachylenia przekątnej ściany bocznej i
sąsiedniej ściany bocznej
A mianowicie :
W graniastosłupie prawidłowym trójkątnym tg kąta nachylenia przekątnej ściany bocznej i
sąsiedniej ściany bocznej  Czyli policzyć tg α
Czyli policzyć tg α  Dzięki za pomoc
Dzięki za pomoc 

 Nie jestem pewien lecz nie powinno być tak?
Nie jestem pewien lecz nie powinno być tak?





 a−krawędź podstawy
d−przekątna ściany bocznej
x−szukany kąt
a−krawędź podstawy
d−przekątna ściany bocznej
x−szukany kąt


 A ma być do ... sąsiedniej ściany bocznej.
A ma być do ... sąsiedniej ściany bocznej.
 Ehh no faktycznie ale wiem jak to naprawic
Ehh no faktycznie ale wiem jak to naprawic  wiec to chyba ostateczna wersja
wiec to chyba ostateczna wersja  − zadanie z
podstawy chyba?
− zadanie z
podstawy chyba?


 czyli też źle
czyli też źle 

 Dziękuję Rivi
Dziękuję Rivi






