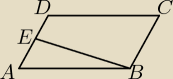
Proszę o pomoc Absolwent :): Proszę o pomoc w rozwiązaniu tych dwóch zadań Zad.1 Punkt E jest środkiem boku AD równoległoboku ABCD (patrz rys. wyżej). Pole trójkąta ABE jest równe 2. Oblicz pole równoległoboku. Zad.2 Wyznacz największą wartość funkcji f(x) = −x² +3x−2 w przedziale <−1,2>

Absolwent :):

	3		1
W tym Zad.2 jak liczyłem to mi wyszło, że wierzchołek paraboli będzie w pkt. (		,		).
	2		4

Grześ: Zad. 1 |AD|=x

	1
|AE|=		x
	2

Między AD a AB jest kąt alfa, więc pole trójkąta wyraża się wzorem:

	1
P1=sinα*		x*|AB|
	2

A pole równoległoboku: P₂=sinα*x*|AB|=2*2=4

Kejt: 2. f(x)=−x² +3x−2 Δ=3²−4*2=1

	−1
q=		=1
	−4

	−3
p=		=1,5
	−2

Kejt: taak..

	1
q=		oczywiście..
	4

Absolwent :): Kejt, ale w odpowiedzi co trzeba napisać?

Kejt:

	1
f(x)max=		..?
	4

Absolwent :):

	1
Też bym tak napisał . I wyszło mi tak jak Tobie . Wystarczy napisać, że fmax=		?
	4

Kejt: tak mi się wydaje.. słownie też można..

Absolwent :): A w tym też byś tak zrobiła: Rozwiąż równanie: x³−5x²−3x+15=0 x²(x−5)−3(x−5)=0 (x²−3)(x−5)=0 (x+√3)(x−√3)(x−5)=0 x=√3 ⋁ x=−√3 ⋁ x=5 ? Tylko nie jestem pewny czy może być, że x=−√3 Jak to będzie?

Absolwent :): ?

Kejt: największa wartość tej funkcji?

Absolwent :): Nie to jest kolejne zadanie co Ci wyżej napisałem

Kejt: "A w tym też byś tak zrobiła: " co sugerowałoby takie samo polecenie.. mam do tego odpowiedź Ci napisać?

Absolwent :): Polecenie do tego wyżej zadania jest takie Rozwiąż równanie . No i w zasadzie to chcę wiedzieć czy dobrze to rozwiązałem . No, bo nie jestem pewny

Kejt: W(x)=x³−5x²−3x+15 W(x)=0 <=> x∊{−√3;√3;5}

Kejt: jest dobrze.

Absolwent :): no to spoko

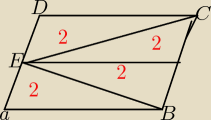
Murzynek: A czemu tak nie może byc..?

Don: up

Mateusz: Mi się wydaje, że Grześ źle policzył... Bo wzór na P1 powinien być:

1		1		1		1
	sinα*|AE|*|AB| =		sinα*		x*|AB| =		sinα*x*|AB|
2		2		2		4

1
	sinα*x*|AB| = 2
4

to sinα*x*|AB| = 2*4 = 8 i chyba takie jest pole równoległoboku?

tom215: Mateusz dobrze to wyliczył ale rozumowanie Murzynka tez jest wg mnie prawidłowe, bo równoległobok ma po 2 pary tych samych boków i 2 pary równych katów