Równanie z parametrem Nie jestem mądry: Określ liczbę pierwiastków równania 2x²−5IxI−m=0 w zależności od parametru m.

Murzynek: popieram to pytanie.

Grześ: 2x²−5|x|=m Narysuj funkcję f(x)=2x²−5|x| i graficznie sprawdzaj przedziałąmi

Rivi: Δ=25+8m jak Δ>0 to 2 roz jak Δ=0 to 1 rozw, jak Δ<0 brak można deltę mimo, że jest bezwzględna, no bo czy jest tam 5x czy −5x nie gra w delcie roli, bo jest do do kwadratu robione. Z wykresu... może być trudno

Grześ: tak nie zrobisz... albo graficznie, albo rozbijanie na wiele przypadków

Grześ: z wykresu właśnie łatwo, wystarczą 3 szczególne punkty: 2 miejsca zerowe, wierzchołek przekształconej paraboli.

stokrotka: według mnie Rivi ma racje. bo dla x<0 2x²+5x−m=0 a dla x≥0 2x²−5x−m=0 i ta "5" nie gra w Δ roli a mamy tylko podac kiedy Δ> 0 Δ=0 i Δ<0 .. a z rysunku to ciezko nawet by bylo naniesc to.. brzydkie rzeczy wychodzą.

Grześ: oj a nie widzicie wartości bezwzględnej rozbijesz na przypadki, ale potem ich sie musicie trzymać, bo Δ>0 gwarantuje wam dwa pierwiastki, ale nie muszą być w przedziale x∊(0,+∞), to nie taka prosta sprawa

Rivi: Jednak nie można tak... dla m=−3,125 2 roz m∊(−3,125,0) 4 roz, m=0 3 roz i powyżej 0 4 rozw. Z rysunku. Delta jest ta sama... ale wychodzą inne współrzędne wierzchołków, i ilość rozwiązań

jest podwojona. (prócz m=0 gdzie jedno rozwiązanie te parabole mają wspólne)

Zwracam honor

Grześ: widać wrzuciłeś do wolframu gratuluje

Rivi: Nieee.. wrzuciłem do mojego zeszyciku

Grześ: dobra, żartuje... więc są 3 sposoby: jeden graficzny, algebraiczny(podstawienie t=|x| i korzystanie z delty i wzorów Viete'a oraz drugi algebraiczny, wg mnie trudniejszy, na dwóch przedziałach x<0 i x≥0

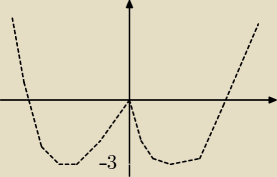
Artur: schematycznie, dla m<−3 brak rozwiązan m = −3 dwa rozwiązania m>−3 m<0 4 rozwiązania m=0 3 rozwiązania m>0 2 rozwiązania

Nie jestem mądry: Dzieki bardzo