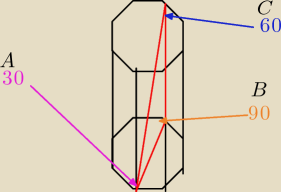
graniastosłup Mateusz: W graniastosłupie prawidłowym sześciokątnym kąt nachylenia krótszej przekątnej do płaszczyzny podstawy jest równy 30^o. Wiedząc, że objętość graniastosłupa jest równa 12√3, oblicz długość krótszej przekątnej. Rysunek mojego autorstwa i chyba poprawnie oznaczone? V=Pp*h V=12√3 12√3=Pp*h Podstawa to sześciokąt foremny czyli 6 trójkątów równobocznych:

	a2√3
Pp=6*
	4

	a2√3
12√3=6*		*h |*4
	4

48√3=6*a²√3*h | /√3 48=6*a²*h | /6 8=a²*h |AB|=2a więc z trójkąta 30 60 90 można policzyć |CB| które jest naszym h

	√3
2a=		x | *2
	2

h=0,5x 4a=√3x | /√3 h=0,5x

	4√3a
x=
	3

h=0,5x

	4√3a		2√3a
h=0,5 *		=
	3		3

No to podstawiam h do tego co miałem wcześniej: 8=a²*h

	2√3a
8=a2*		| *3
	3

24=a²*2√3a | /2√3

	24
a3=
	2√3

a³=4√3 i czy to się trzyma kupy? bo przecież z trójkąta 30 60 90 wynika, że x=a czyli wynik wyjdzie dość dziwny oO

Kejt: to nie jest krótsza przekątna tylko dłuższa..

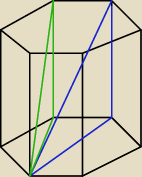Kejt: zielone − krótsza przekątna niebieskie − dłuższa przekątna mam nadzieję, że jasne..

Mateusz: też to zauważyłem jak wziąłem sobie model bryły i liczę wszystko na nowo, mam nadzieję, że teraz wyjdzie

Kejt: jakby nie wyszło to mów..zobaczymy co da się zrobić

Mateusz: Długość krótszej przekątnej wyszła mi 4 więc chyba dobrze...