Aldo:

	→
W kwadracie ABCD dane są A=(1,0),		[8,4]. Wyznacz równania prostych, w których zawarte
	AC

są przekątne tego kwadratu. No więc na początek wyznaczam punkt C(9,4). I odpowiednio rysuję sobie prostokąt. Zaznaczam przekątne. Obliczam punkt przecięcia tych przekątnych (czyli układ równań dwóch prostych (przekątnych prostokąta), lub odczytuję z wykresu. Co lepiej pod maturę rozszerzoną ?) Skoro mam współrzędne środka przekątnych : S(5,2) to rysuję dwa do góry i dwa na dół na osi Oy. Wyznaczam punkty kwadratów, i mam kwadrat o bokach : A(1,0)B(5,0), C(5,4) D(1,4). Rysuję przekątne i wyznaczam równanie prostej przechodzącej przez AC i BD. Czy takie rozwiązanie jest poprawne? Czy powinienem to jakoś inaczej zrobić? Jestem bardzo słaby z geometrii analitycznej. Proszę o pomoc

Aldo:

Aldo: Proszę, zerknijcie ktoś na to zadanie. Ono jest za 4 punkty. A nie mogę sobie z nim poradzić.

Aldo:

Aldo:

Aldo: Zerknijcie ktoś na to zadanko.

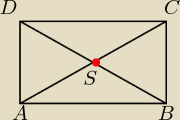
Klaudia: Nie rysuj "dwa w górę i dwa w dół" bo możesz stracić punkt. Poprowadź przekątną DB przechodzącą przez punkt S. Wyznacz współrzędne punktu D dzięki wiadomości, że wektor DB jest skierowany w dół czyli jego współrzędne to DB=[8,−4]. DS= ¹₂ DB DS=[¹₂*8,¹₂*−4] DS=[4,−2] wektor DS=[5−x_d,2−y_d] DS=[4,−2]⇔ 5−x_d=4 i 2−y_d=−2 x_d=1 y_d=4 D(1,4) Tak samo liczysz B. To znaczy BS to jest połowa wektoru DB. Potem liczysz punkt B tak samo jak ja liczyłam punkt D. Po wyliczeniu wszystkich punktów wyznaczasz proste przechodzące przez przekątne kwadratu. Punkty A(1,0); B(9,0); C(9,4); D(1,4). Wyznaczasz równania prostych AC i BD.

Aldo: ok, dziekuje Ci bardzo

Artur: wystarczyło napisać równanie prostej nachylonej do osi OX pod kątem tg45* przechodzącą przez pkt A i potem prostą padającą pod katem prostym do niej przechodzącą przez srodek AC

Doma: Dlaczego ten prostokąt jest kwadratem

:D:D: Pozdrawiam uczniów mistrza Marka! Wiem, że stąd spisujecie