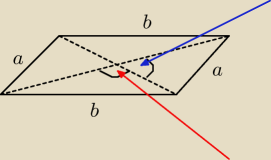
Pytanie Jordan: Dany jest równoległobok jak na rysunku. I moje pytanie brzmi czy znając cosinus kąta zaznaczony czerwoną strzałką jestem w stanie korzystając tylko z tej informacji obliczyć cosinus kąta oznaczonego niebieską strzałką ?

Kejt: znając cosinus sprawdzasz w tablicach miarę kąta i odejmujesz od 180^o. i masz miarę drugiego kąta..sprawdzasz w tablicach wartość cosinusa dla takiej miary kąta

Godzio: cosα = a cos(180 − α) = − cosα = −a Teraz jasne ?

Jordan: o kurcze racja dzięki Godzio, ale mam jeszcze jedno pytanie: sin(180 − 3α) = sin3α dlaczego tyle a nie −sin3α

Godzio: 180 − 3α to 2 ćwiartka, a tam sinus jest dodatni, dlatego nie ma przeciwnego znaku

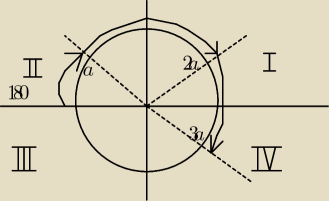
Jordan: właśnie dlaczego II cwiartka ja jak zaczynam liczyć taki przykład to robie tak jak na rysunku a = alfa

Godzio: Wiesz co, powiem Ci jak ja to rozumiem Jeśli mamy dowolny kąt x (x = α, x = 5α itd) to zakładam, że on jest zawsze kątem ostrym (x < 90) sin(180 − x) = jeśli od 180 odejmiemy kąt ostry to będziemy w 2 ćwiartce, a tam sinus jest dodatni Tak samo cos(270 − x) = − sinx bo jeśli od 270^o odejmiemy kąt ostry x to będziemy w 3 ćwiartce (zmiana funkcji jest dlatego, że jest nieprzysta liczba 90^o) Dla mnie to jest najłatwiej w ten sposób to rozumieć, nie musi być to koniecznie po matematycznemu bo np. sin(180^o − 120^o) = sin(120^o) (więc to działa dla dowolnego kąta, tyle, że później będzie trzeba to wyliczać

Jordan: czyli bez względu na to czy jest (180 − α), (180 − 3α) czy (180 − 20α) to w tym przypadku zawsze będzie w drugiej cwiartce ? Bo wiesz jak by zamiast tej 3 na poczatku było alfa to bym zrobił właśnie tym twoim sposobem

Godzio: Tak, zawsze w 2 ćw. ale dla konkretnego kąta może się to nie zgadzać, chodź wzór dalej będzie prawdziwy

Jordan: o to mi chodziło dzięki bardzo Pozdrawiam