 P(x)=P(ΔABN)= 36 −[P(ΔKAN) +P(ΔALB) + P(BMN)]
|KA|= x , x >0
P(x)=P(ΔABN)= 36 −[P(ΔKAN) +P(ΔALB) + P(BMN)]
|KA|= x , x >0
| 3x(6−x) | ||
P(x)= 36 −[ 3x + | + (2−x)*9] dla x€ (0,2)
| |
| 2 |
| 3 | ||
P(x)= ................... = | x2−3x+18 −−−− f. kwadratowa ,parabola ramionami do góry
| |
| 2 |
| −b | 3 | |||
dla xw= | = | = 1 | ||
| 2a | 3 |



 To zadanie miałem jako jedno z 1 na fakultetach
To zadanie miałem jako jedno z 1 na fakultetach  , najtrudniejsze dla mnie było "Oblicz
długość |KA|, dla którego pole trójkąta NAB jest najmniejsze."
, najtrudniejsze dla mnie było "Oblicz
długość |KA|, dla którego pole trójkąta NAB jest najmniejsze."
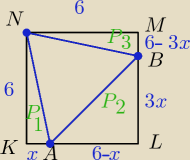 Pole kwadratu to 36
P1=6 * x* 12 = 3x
P2=(6 − x) * 3x * 12 = 9x −32 x2
P3=6 * (6 − 3 x ) * 12= 18 − 9x
od Pola kwadratu gdy odjąc pola tych trzech trójkątów i otrzymam pole trójkata NAB
36 − ( 3x + 9x − 32 x2 + 18x −9x)
36 − ( − 32 x2 +3x + 18)
36 + 32 x2 − 3x − 18
32 x2 − 3x + 18
funkcja jest rosnąca więc najmniejszą wartość przyjmuje dla pierwszej współrzędnej wierzchołka
p = −b2a = 3 * 23 = 2
odp Dla KA równego 2 pole trójkąta NAB jest najmniejsze
dobrze to zrobiłem?
Pole kwadratu to 36
P1=6 * x* 12 = 3x
P2=(6 − x) * 3x * 12 = 9x −32 x2
P3=6 * (6 − 3 x ) * 12= 18 − 9x
od Pola kwadratu gdy odjąc pola tych trzech trójkątów i otrzymam pole trójkata NAB
36 − ( 3x + 9x − 32 x2 + 18x −9x)
36 − ( − 32 x2 +3x + 18)
36 + 32 x2 − 3x − 18
32 x2 − 3x + 18
funkcja jest rosnąca więc najmniejszą wartość przyjmuje dla pierwszej współrzędnej wierzchołka
p = −b2a = 3 * 23 = 2
odp Dla KA równego 2 pole trójkąta NAB jest najmniejsze
dobrze to zrobiłem?

| −b | |
=............ =1 | |
| 2a |
| −b | ||
p = | = nie podzieliłeś | |
| 2a |

 .
.