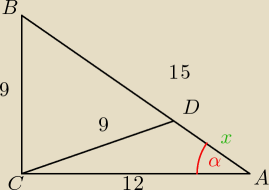
Brygida :): W trójkącie prostokątnym ABC przyprostokątne mają długości : |BC|=9, |CA|=12. Na boku AB wybrano punkt D, taki że odcinki BC i CD mają równe długości. Oblicz długość odcinka AD. Ja to zadanie zrobiłam z twierdzenia cosinusów. Na początku z tw. pitagorasa obliczam |AB|=15. zał: x<15. Teraz skoro mam podane wszystkie długości boków to korzystając z twierdzenia cosinusów obliczam kąt α. Z tw. cosinówsów dla ΔABC 9²=12²+15²−2*12*15*cosα 81=144+225−360cosα

288
	=cosα
360

	4
cosα=
	5

Teraz korzystając ponownie z twierdzenia cosinusów dla ΔDCA obliczam x.

	4
92=122+x2−2*12*x*
	5

	96x
81=144+x2−
	5

	96x
81−144=x2−
	5

5x²−96x+315=0 Δ=54 x1=4,2 x2=15 − odrzucamy, ponieważ z założenia wynika, że x<15. Czy to zadanie jest poprawnie wykonane? Czy jest jakaś inna metoda na wyliczenie tego? Bo w tej łatwo o pomyłkę. Dziękuję i proszę o sprawdzenie. Pozdrawiam

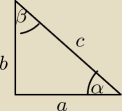think: Kochana gdyby Gustlik To zobaczył to miałby używanie funkcje trygonometryczne w trójkącie prostokątnym są dużo prostsze

	b
sinα =
	c

	a
cosα =
	c

	a
sinβ =
	c

	b
cosβ =
	c

na prawdę mogłaś sobie darować liczenie z tw. cosinusów acz jak sprawdzisz wykonałaś obliczenia poprawnie

think: w drugiej części użycie twierdzenia cosinusów było jak najbardziej uzasadnione i właściwe

Bogdan:

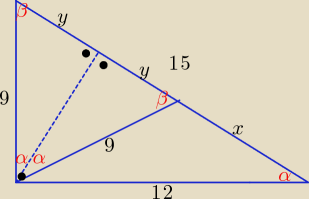
y		9
	=		⇒ y = 5,4
9		15

x = 15 − 2y = 15 − 10,8 = 4,2

Gustlik: Think, ja taki straszny nie jestem, aczkolwiek Brygida pojechała sobie dookoła świata, niemniej dość ciekawa metoda, fajny sposób wymyślił Bogdan. Pozdrawiam

Brygida :): A tam. Czepiacie się. A żebyś Gustlik wiedział, że lubię podróżować. To dlatego tak naokoło. Dziękuję Bogdanie za mikroskopijne pod względem zajętej powierzchni rozwiązanie. Postaram się je zapamiętać, bo na maturze szkoda troszkę czasu na moje obliczenia. Nie zapominam również o Tobie Think − również dziękuję za Twoje rozwiązanie Pozdrawiam