trapez em: Jak wykazać, że jeżeli przekątna trapezu (równoramiennego?) jest prostopadła do ramienia, to ramiona i krótsza podstawa są równe?

Artur: hmm...pewnie da się na tym opisać okrąg, będzie kąt prosty wtedy jak podstawa trapezu będzie srednicą, będzie kąt prosty, a zarazem dwa ramiona i górna podstawa podzieli nam półkole na 3 równe częsci...

em: hmm... brzmi logicznie. ale jak to sensownie zapisać?

b.: tego nie można wykazać, bo to nieprawda − spróbuj narysować kontrprzykład (wsk. post Artura )

em: nieprawda? przecież to jedna z własności trapezu

b.: przybliżony rysunek

:): ale ten kąt nie jest prosty, widzisz?

b.: mniej więcej jest. kontrprzykład można porządniej narysować rysując okrąg, tak jak pisał Artur

em: jej... ale to nie może być mniej więcej... p.s. ja nie pytam czy to jest prawda, proszę tylko, żeby ktoś pomógł mi to wykazać

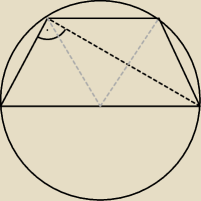
Artur: no i powstają 3 trójkąty równoboczne...

em:

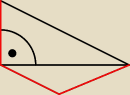
em: owszem, są równoboczne a myślisz, że to jedyny sposób, na wykazanie tego?

PanCogito:

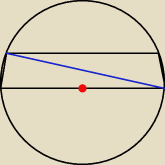
b.: 1. rysujesz okrąg i średnicę, ta średnica będzie dłuższą podstawą trapezu 2. rysujesz odcinek o końcach na okręgu, równoległy do średnicy i dość blisko środka okręgu. To będzie krótsza podstawa. I już. Na rysunku może być mniej więcej, chodzi o ideę, która miałem nadzieję, że będzie jasna... no ale jednak nie była...

em: wiesz, jakoś nie mogę się do tego przekonać. ale chyba jednak muszę przyznać, że masz rację