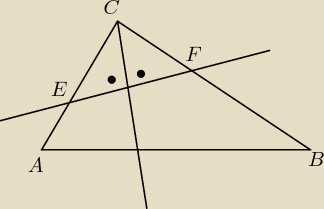
wykaż Joanna: W trójkącie ABC poprowadzono dwusieczną kąta C, a następnie narysowano prostą m prostopadłą do tej dwusiecznej, która przecięła boki AC i BC trójkąta odpowiednio w punktach E i F. Wykaż, że trójkat EFC jest równoramienny.

Joanna:

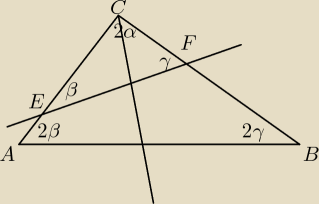
Joanna: Próbowałam zrobić tak: dla trójkąta ABC: 2α + 2β + 2γ = 180^o dla trójkąta CEF: 2α + β + γ = 180^o Chciałam podstawić: 2α + β + γ = 2α + 2β + 2γ 2β − β = −2γ + γ β = −γ Wiem, że to głupota ale nie wiem gdzie błąd jest

Joanna: Pomoże ktoś?

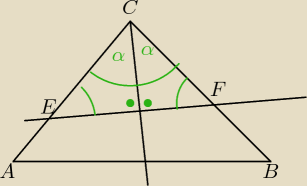
PanCogito: Kąty przy podstawie są takie same więc trójkąt jest równoramienny

Joanna: Coś więcej? Bo raczej to nie starczy nauczycielowi.

Joanna: Pomocy

Maryjusz: Musi mu to wystarczyć.

Maciuś: PanCogito nic nie wykazales tym stwierdzeniem

Joanna: Ale to jest aż za proste

Joanna: Jak nic nie wykazał?

Joanna: Dwusieczna dzieli na dwa równe kąty, ∡C początkowo miało 2α po puszczeniu dwusiecznej, zostało po jednej stronie jedno α i po drugiej stronie drugie α. Patrząc na to, że tam jest kąt prosty więc po dwóch stronach dwa kąty są takie same więc β = γ. (β po lewej stronie, γ po prawej ) Tak o chyba

Joanna: Może być? Wolałaby aby potwierdził to jakiś expert.

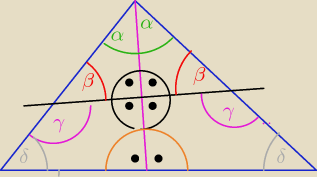
Maciuś: kat β musi byc rowny skoro to jest dwusieczna kata to α + kat prosty ktory powtaje przez przeciecie prostopadle.Te boki β i γ sa przystajace czyli 180− β =γ po obu stronach musza byc takie same . Jak idzisz powstaja 2 podobne trapezy o 3 katach takich samych czyli 4 kat musi byc taki sam jak obok . Wlasnie udowodnilas ze trojkat jest rownoramnienny

PanCogito:

PanCogito: Maciuś zbyt komplikujesz banalne zadanie

Maciuś: pan cogito ale nic tym nie osiagniesz nadal boki moga katy przy boku E i Fmoga byc rozne nie udowadniasz tym tego swoim rysunkiem

Joanna: Tak jak napisałam ?

Joanna: PanaCogito rozumiem, a Maciuś gmatwa za bardzo.

PanCogito: Jak mogą by różne? Kat DEC = 180−90−α Kat DFC = 180−90−α

Maciuś: Joanna rob jak chcesz pan cogito nie wykazal w kazdym badz razie tej tozsamosci bo on od razu przyjal ze dwusieczna pada pod katem prostym do podstawy a tego nie wiadomo

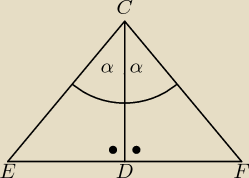
PanCogito: Dwusieczna jest prostopadła do prostej m Punkty E D F leżą na prostej m. Podstawą się nie zajmujemy

Joanna: Maciuś rysunek był taki jak na górze. I tam był przecież zaznaczony kąt prosty przy przecięciu tej prostej z dwusieczną i z tego skorzystał PanCogito. Zauważył, że skoro po jeden stronie jest 90^o to po drugiej stronie też musi być. W trójkącie ABC można oznaczyć przy wierzchołku C kąt 2α, jak puścimy dwusieczną to podzieli na dwa równe kąty więc po jeden stronie będzie α i po drugiej. Czyli mamy już po jednej stronie dwa takie same kąty i po drugiej więc, te trzecie też są równe. (w sensie równe sobie )

Maciuś: nie musial byc zaznaczony bo to wiadome ze prosta rownolegla przecina pod katem prostym . Ale wytlumacz mi skad wiesz ze katy przy A I B sa takie same , tylko wtedy bedzie wykazana zleznosc

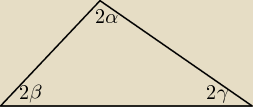
Joanna: Oznaczyłam sobie na początku:

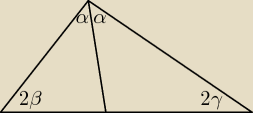
Joanna: Dwusieczna dzieli kąt na dwa RÓWNE kąty więc zostaje

Maciuś: sama teraz wlasnie napisalas sprzecznosc ktora przekresla ta zaleznosc bo jezeli 2β ≠ 2γ to jaki sposob ma byc to trojkat rownoramienny? Przypomne ze trojkat rownoramienny to taki ktory w podstawie ma 2 katy tej samej miary i jeden lezacy naprzececiwko innej miary

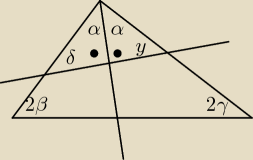
Joanna: Następnie puszczamy prostą i już widać, że po jeden stronie jest α i 90^o oraz po drugiej to samo więc kąty δ i y są równe

Joanna: Te kąty które ci tam zaznaczyłam nie są ważne bo nie ten trójkąt mamy udowodnić, że jest równoramienny. Tylko Ten mniejszy.

Maciuś: Asiu skarbie Ja to rozumiem ale ty nie wykazujesz i pan cogito na tym rysunku ze katy w twoim oznaczeniu 2β i 2γ ze sa rowne?

Maciuś: aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa kurde najmocnej przepraszam ja myslalem ze trzeba ten najwiekszy sorry

Joanna: Ale kąty 2β i 2γ nie są do niczego potrzebne

Maciuś: W takim razie to banał Tak tak przepraszam jak to zawsze nie doczytalem zadania Przepraszam jeszcze raz za zamieszanie

Maciuś: Ale cogito tez myslal ze ten duzy

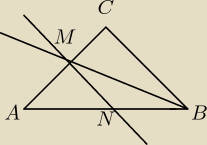
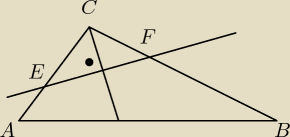
Joanna: Wiesz może jak zrobić coś takiego: W trójkącie ABC dwusieczna kąta B przecina bok AC w punkcie M. Przez punkt M prowadzimy prostą równoległą do BC, przecinającą bok AB w punkcie N. Udowodnij, że |MN| = |BN|

Maciuś: daj mi chwile mysle ze twierdzenie tallesa da rade

Maciuś: ^|AN|_|MN|=^|AN|+|NB|_|CB|

Joanna: Możesz to zapisać z U { } { } (bez spacji)

Maciuś:

|AN|		|AN|+|NB|
	=
|MN|		|CB|

Joanna: I co dalej ?

Joanna: Halo

Maciuś: rozpisalem ci przeciez

Maciuś:

a		a + c
	=		⇒ad=ba+bc ty masz sprawdzic czy "a" jest rowne "c"
b		d

Maciuś: aa sory ty masz sprawdzic czy b jest rowne c

Joanna: wiec?

Joanna: Nie da się tego z Talesa udowodnić

Maciuś: jak nie da sie?

Maciuś: ad=ba+bc : | b

ad
	=a+c : | −a
b

ad
	−a=c
b

ad		ad		ad		ad
	=a+		−a ⇔		=
b		b		b		b

Natalia: no ale doprbze było napsiane zdecydowanie wyżej, sa dwa katy α potem sa dwa katy proste a wiec kat 3 w trojkacie CES (s−punkt przeciecia tych prostych) jest rowny katowi 3 w trojakcie CFS skor katy przy podstawie sa rowne to musi to byc rownoramienny

Maciuś: Natalia ja nie doczytalem tresci myslalem ze chodzi o ten duzy bo ten maly wykazac to banal

Joanna: Możesz to zapisać w takiej formie jak to wyzej? |NM| itp?

Natalia: to juz wszytko wiemy

Natalia: juz sie robi

Natalia: przyjmijmy ze s jest kątem przeciecia tej dwusiecznej z prsota EF wtedy ∡ECS=α i ∡FCS=α wiemy ze prosta EF jest prstopadla do dwusiecznej czyli∡CSE=90st i ∡CSF=90st ∡CES=90st−α i∡CFS=90st−α z tego wynika ze te katy sa rowne czyli trojkat CEF jest rownoramienny bo katy przy podstawie EF sa sobie rowne

Natalia: poprawka S jest punktem, przepraszam

Maciuś: Joanna now wiesz co? nawet tego ci sie nie chce zrobic? masz cale zadanie rozwiazene i nie chce ci sie popodstawiac? a=|AN| b=|MN| c=|NB| d= |CB|

Natalia: na maturze tak byloby na maxa czyli prawdopodbnie na 2pkt bo takie zadania sa zawyczaj za 2pkt

Maciuś: Natalko skarbie to zadanie co sie niepotrzebnie trudzisz dawno jest wyjasnione

Joanna: Własnie Macius robiłam ale mi nie wychodzi, na samych a, b, c, d owszem ale jak już z tymi kreskami to się gubię

Maciuś: pod a wstawiasz |AN| pod b wstawiasz |MN| pod c |NB| pod d |CB| nie chce mi sie tego pisac ide poogladac film pozdrawiam