... chomik: Proszę was o pomoc, chociarz o dobry rysunek, bo mi coś nie wychodzi Zpunktu C leżącego na okręgu o promieniu r= 10 poprowadzono dwie cięciwy CA i CB równej długości. KAT ACB ma mmiare α= 30 stopni. Oblicz pole trójkąta ABC.

Mati: Masz trójkąt równoramienny z podstawą 20 i kątem 30'

ICSP: Dlaczego podstawa ma mieć 20 Twierdzenie sinusów proponuję.

Matt: Chyba coś nie

chomik: ISCP czy ten rysunek jest dobry? a do twierdzenie potzrebuje chyba dwa kąty i jedną odległość prawda?

ICSP: przecież masz promień okręgu opisanego. Co do rysunku to rzeczywiście jest dobry.

chomik: ale prosta ab nie jest średnicą okręgu, więc jak moge wykorzystć promień

ICSP: widzę że twierdzenia sinusów dokłądnie nie znasz.

a		b		c
	=		=		= 2R gdzie R jest promieniem okręgu opisanego na tym
sinα		sinβ		sinγ

trójkącie.

chomik: kurcze, nie rozumiem mógłbyś zrobić chociaż kawałek to może zajaże

chomik: w zadaniu kąt alfa = 30 stopni z rysunku wynika że ma około 90 stopni

ICSP: rysunek nie musi być dokładny. Ważne aby obrazował tobie co masz obliczyć.

Matt:

|AB|
	= 20
0,5

|ab| − podstawa. 0,5 − wartosć sinusa. 20 = 2R.

chomik: cab

chomik: Dacie rade coś wymyślić

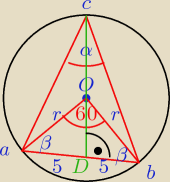tomek: ja takie cos wymyśliłem Jak widzimy to jest kąt wpisany w okrąg i kąt środkowy oparty na tym samym łuku, czyli kąt środkowy wynosi 60 stopni ponieważ α = 30 stopni, ponadto ramiona powstałego trójkąta aOb są takie same czyli jest równoramienny. CZyli kąty przy podstawie sa równe a to proste obliczenia 2β= 180 − 60stopni czyli β = 60 stopni z czego wynika ze ten trójkąt aOb jest równo ramienny czyli podstawa trójkąta abc jest równa 10 wiemy że wysokość od srodka okręgu do punktu c to promien okręgu czyli 10 potrzeba nam jeszcze druga czesc, od punktu O do punktu D obydwa odcinki leża na tej samej prostej ponieważ oba trójkąty oparte sa na tej samej podstawie oraz nie zapominajmy o tym ze to kąt środkowy i wpisany oparty na tym samym łuku

	|OD|
korzystamy z twierdzenia pitagorasa tgβ =
	5

z czego wynika nam ze |OD| = 5√3 natomiast cała wysokosc to 10 + 5√3 mamy podstawe, mamy wysokosc − liczymy pole

	10+ 5√3 * 10
PΔABC =		= 50 + 25√3 = 25(2 + √3)
	2