Natalia:
policzylam najpierw zadanie dla P(B−A)= 0,3 ale wychodzila mi sprzecznosc wiec policzylam dla
P(B−A)=0,03 a wiec
P(A∩B)=a
1
P(A)=a
3=a
1+2r
P(B)=a
4=a
1+3r
P(A∪B) = 0,65
P(A∪B) = P(A)+P(B)−P(A∩B)
0,65=a
1+2r+a
1+3r−a
1
0,65=a
1+5r
P(B−A) = 0,03
0,03=a
1+3r−a
1−2r
0,03=r
podstawiamy do powyzszego
0,65=a
1+0,15
a
1=0,5 =P(A∩B)
a
3=0,56 =P(A)
a
4=0,59
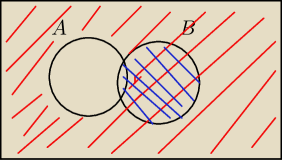
i teraz potrzebujemy rysunku
Mamy policzyc P(A'∪B) z rysunku wynika ze P(A'∪B) to jest czesc P(B) bez czesci wspolnej ze
zbiorem A czyli
P(A'∪B)=P(B)−P(A∩B)=0,59−0,5=0,09
jesli tlyko ovzywiscie tam jest 0,03 dla kotrego policzylam to wszytko sie zgadza ale ejsli
jest 0,3 to wychdozi sprzecznosc
 policzylam najpierw zadanie dla P(B−A)= 0,3 ale wychodzila mi sprzecznosc wiec policzylam dla
P(B−A)=0,03 a wiec
P(A∩B)=a1
P(A)=a3=a1+2r
P(B)=a4=a1+3r
P(A∪B) = 0,65
P(A∪B) = P(A)+P(B)−P(A∩B)
0,65=a1+2r+a1+3r−a1
0,65=a1+5r
P(B−A) = 0,03
0,03=a1+3r−a1−2r
0,03=r
podstawiamy do powyzszego
0,65=a1+0,15
a1=0,5 =P(A∩B)
a3=0,56 =P(A)
a4=0,59
i teraz potrzebujemy rysunku
Mamy policzyc P(A'∪B) z rysunku wynika ze P(A'∪B) to jest czesc P(B) bez czesci wspolnej ze
zbiorem A czyli
P(A'∪B)=P(B)−P(A∩B)=0,59−0,5=0,09
jesli tlyko ovzywiscie tam jest 0,03 dla kotrego policzylam to wszytko sie zgadza ale ejsli
jest 0,3 to wychdozi sprzecznosc
policzylam najpierw zadanie dla P(B−A)= 0,3 ale wychodzila mi sprzecznosc wiec policzylam dla
P(B−A)=0,03 a wiec
P(A∩B)=a1
P(A)=a3=a1+2r
P(B)=a4=a1+3r
P(A∪B) = 0,65
P(A∪B) = P(A)+P(B)−P(A∩B)
0,65=a1+2r+a1+3r−a1
0,65=a1+5r
P(B−A) = 0,03
0,03=a1+3r−a1−2r
0,03=r
podstawiamy do powyzszego
0,65=a1+0,15
a1=0,5 =P(A∩B)
a3=0,56 =P(A)
a4=0,59
i teraz potrzebujemy rysunku
Mamy policzyc P(A'∪B) z rysunku wynika ze P(A'∪B) to jest czesc P(B) bez czesci wspolnej ze
zbiorem A czyli
P(A'∪B)=P(B)−P(A∩B)=0,59−0,5=0,09
jesli tlyko ovzywiscie tam jest 0,03 dla kotrego policzylam to wszytko sie zgadza ale ejsli
jest 0,3 to wychdozi sprzecznosc