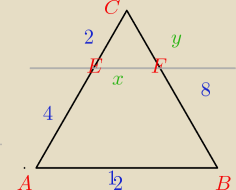
... niedouczony: W trójkącie dane są; IABI= 12 IACI = 6 IBCI= 8ABFE14xy. poprowadzono prostą równoległą do boku AB, która przecina bok AC w punkcie E odległym od kunktu C o 2, a bok BC przecieła w punkcie F. wyznacz obwód trójkąta EFC. ( trójkąt ten nie jest równoboczny, tak ja go tylko narysowałem) ja wyliczyłem sobie x i y z proporcji i wyszło mi x=6 , zaś y= 4 czy to jest dobrze, jak jest coś zle prosze o poprawienie

DasAuto: Wszystko dobrze obliczyłeś

niedouczony: obwód trójkąta EFC mi wyszedł 12 zaś w odpowiedziach jest ²⁶₃

DasAuto: Podziel 26 przez 3 hehe

DasAuto: Nie wiem niby wszystko dobrze

niedouczony: No właśnie niby, ale jest raczej źle, ale gdzie jest bląd

DasAuto:

	2		6
y wyliczasz zapisując proporcję		=
	y		8+y

rumpek: Jak jeszcze nie zrobione to mogę pomóc

rumpek: Wynik podręcznikowy dobry jest

DasAuto: Dawaj rumpek ja już mam dość matmy na dziś

rumpek: ok

niedouczony: bardzo prosze o pomoc Rumpku, wydaje sie że wszystko jest dobrze a jest źle:( DasAuto, 8 odnosi sie do odcinka ICBI tak jest w poleceniu IABI = 12 IBCI = 8 IACI= 6

DasAuto: aaa no widzisz myślałem że I BF I = 8 no to już wiem gdzie jest bład

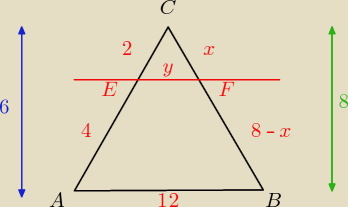
rumpek: Z twierdzenia Talesa mamy proporcję:

2		x
	=
4		8 − x

2 * (8 − x) = 4x 16 = 6x

	16		2
x =		= 2
	6		3

Można też inną proporcją z Talesa:

2		x
	=
6		8

6x = 16 / : 6

	2
x = 2
	3

To mamy już x, teraz y: z podobieństwa trójkątów:

2		6
	=
y		12

6y = 24 / : 6 y = 4

	2		2		26
L = 2 + 2		+ 4 = 8		=
	3		3		3

DasAuto: Właśnie tak

niedouczony: to ja namieszałem, dzięki

grtgr: 67890987654tg∫