wartość bezwzględna Piotrek: Mam raczej takie bardziej pytanie, niż stricte zadanie. Chodzi o to czy w takim równaniu: | |x+3| − 2 | = m mogę "wyciągnąć" minus dwójkę z wartości bezwzględnej ze zmienionym znakiem? Czyli mielibyśmy coś takiego: |x+3| + 2 = m Jeśli mielibyśmy tam plus dwójkę to wtedy wyciągamy ją bez zmiany znaku? Byłbym wdzięczny za wyjaśnienie.

Nie jestem mądry: Mi się wydaje że to będzie coś takiego: dla x∊(−∞,−3) I −x−3−2 I = m dla x∊<−3,+∞) I x+3−2I = m A 2 raczej bym nie wyciągal

Piotrek: Tutaj wyciągają, ale bez zmiany znaku. Dziwne, zawsze wydawało mi się inaczej. https://matematykaszkolna.pl/strona/1106.html

pedros: ja to zawsze w takich pozbywam się 'zewnętrznej' wartości bezwzględnej, czyli w tym przypadku bym porównał do m i −m zgodnie z definicją. Potem już zwykłe równanko z przedziałami.

Piotrek: pedros, tak, z tym, że ja akurat mam przykład, gdzie mam w równaniu dwie wartości bezwzględne. Tylko tutaj dałem taką skróconą wersję. Normalnie to tak leci: | |x+3| − 2 | + | x+1| = m

pedros: ale jaka jest treść zadania? co z tym parametrem?

Piotrek: Dla jakich wartości m to równanie ma dokładnie dwa rozwiązania. W sumie to narysowałem dwa wykresy, ale nigdzie nie ma dokładnie dwóch rozwiązań, dlatego zacząłem się zastanawiać czy mam dobrze. No chyba, że taka jest odpowiedź

Piotrek: A nie, ma. W 0.

pedros: to raczej tak nie będzie, czekaj rozwiążę sobie

pedros: no jak dla mnie to będzie, że dla m∊∅ równanie ma dwa rozwiązania, czyli brak rozwiązań

pedros: tzn nie ma takiego parametru, żeby równanie miało dwa rozwiązania

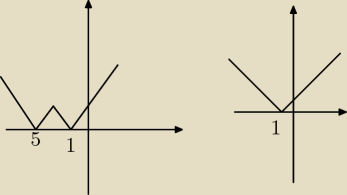
Piotrek: Ale to wychodzi tak jak na tym rysunku, nie? To dla zera powinno być, chyba że jest jakiś motyw z podwójną minus jedynką.

pedros: a jak otrzymałeś ten wykres z lewej strony? bo za bardzo nie wiem skąd to wziąłeś

Piotrek: y=x −−−(sox częściowa)−−−> y=|x| −−−−(translacja[−3,−2])−−−> y=|x+3| − 2 −−−−−(sox częściowa)−−−> y=||x+3|−2|

pedros: a bo to wykres jednego wyrażenia, myślałem, że to całości... tylko, że potem masz jeszcze plus to drugie wyrażenie... hmm stary jeśli mam być szczery to nie wiem, ale jak wpisałem całe wyrażenie w http://www.jogle.pl/wykresy/ wywaliło taki wykres, że nie było by 2 rozwiązań

Piotrek: no, to sie dodaje argumenty obu funkcji.

pedros: no dobra, a podstaw to 0, które otrzymałeś i wychodzi tylko jedno rozwiązanie równania. x=−1 zatem m=0 nie spełnia wymagań zadania. Coś jest nie tak...

Piotrek: A to wiem. Bo z pierwszego wykresu dla −5 y=0, a z drugiego y=4. Więc tam nie ma miejsca zerowego.

Piotrek: zdaje się, że to będzie m∊(0, 4) u (5,∞). Ale może być błąd, bo mam już tak pobazgrane, a nie chce mi sie już przerysowywać.

pedros: bardziej skłonny bym był podejrzewać, że rozwiązaniem będzie przedział m∊(0; 2) tylko nie chcesz mi się sprawdzać

dawid: oblicz pole powierzchni i objetosc stożka ,którego tworząca wynosi 5cm a promień podstawy jest równy 3cm pomocy