Matura rozszerzona
K+K: wrzucam arkusz rozszerzony. Chętnych zapraszam do pomordowania się zad.1
zad.1.
Wyznacz wszystkie wartości parametru m , dla których równanie x
2 + mx + 8 = 0 ma dwa różne
pierwiastki rzeczywiste takie, że suma ich kwadratów jest równa 11m − 34 .
Zad.2.
Funkcja liniowa f określona jest wzorem f(x) = ax + b dla x ∈ R .
a) Dla a = 2008 i b = 2009 zbadaj, czy do wykresu tej funkcji należy punkt P =
(2009,2009
2) .
b) Narysuj w układzie współrzędnych zbiór
| | −1 | |
A ={ (x,y) : x ∈ <− 1,3> i y = |
| x+ b i b ∈ <− 2,1>} . |
| | 2 | |
Zad.3.
Dany jest wielomian W (x) = 8x
3 − 6x
2 + ax + b . Jednym pierwiastkiem wielomianu jest
prawdopodobieństwo otrzymania co najmniej 2 razy orła w trzykrotnym rzucie monetą. Drugi
pierwiastek jest równy prawdopodobieństwu wypadnięcia parzystej liczby oczek na każdej kostce
w rzucie dwiema kostkami. Wyznacz trzeci pierwiastek wielomianu.
Zad.4.
→
Punkt S = (0 ;0) jest środkiem boku AD równoległoboku ABCD . Wiadomo też, że AB = [4;3]
→
oraz BC = [6;2] . Wyznacz wierzchołki tego równoległoboku.
Zad.5.
Ciąg (a,b,c) jest geometryczny i a + b + c = 2 6 , zaś ciąg (a− 5,b− 4,c− 11) jest
arytmetyczny. Oblicz a,b,c .
Zad.6.
Dany jest okrąg o
1 . Kreślimy cięciwę AB nieprzechodzącą przez środek okręgu o
1 , a
następnie rysujemy okrąg o
2 współśrodkowy z okręgiem o
1 i styczny do cięciwy AB . Okręgi
o
1 i o
2 ograniczają pierścień kołowy. Uzasadnij, że pole pierścienia kołowego nie zależy
od długości promienia okręgu o
1 (zależy tylko od długości cięciwy AB ).
Zad.7.
Długości trzech krawędzi prostopadłościanu wychodzących z jednego wierzchołka tworzą ciąg
geometryczny o sumie 19. Objętość prostopadłościanu jest równa 216. Wyznacz pole powierzchni
całkowitej tego prostopadłościanu.
Zad.8.
Jeden z kątów trójkąta prostokątnego ma miarę 60(stopni) , promień okręgu wpisanego w ten
trójkąt ma długość 1. Oblicz długości boków trójkąta.
Zad.9.
W ostrosłupie prawidłowym trójkątnym krawędzie boczne są dwa razy dłuższe od krawędzi podstawy.
1. Wyznacz sinus kąta nachylenia ściany bocznej ostrosłupa do płaszczyzny jego podstawy.
| | 2 | |
2. Wyznacz długość krawędzi podstawy, tak aby objętość ostrosłupa wynosiła |
| √11 |
| | 3 | |
Zad.10.
Dane są zbiory: A = {(x ,y) : x,y ∈ R |x
2 + y
2 |≤ 9} , B = { (x,y) : x,y ∈ R |y| ≤ 1 − x
2
} . Na płaszczyźnie zilustruj zbiory (A ∩ B ) i (A ∩ B′) .
Zad.11.
Wielomian W(x) = (x − 9x + 7)
2005 , po wykonaniu potęgowania i dokonaniu redukcji wyrazów
podobnych, zapisano w postaci W (x) = a
nx
n + a
n−1x
n− 1 + ... + a
2x
2 + a
1x + a
0 .
Oblicz sumę a
n + a
n− 1 + ...+ a
2 + a
1 + a
0 .
proszę też o pomoc ponieważ niektórych zadań nie potrafię zrobić
29 kwi 08:49
kamis:
8.
Oznaczenia:
a − długość przyprostokątnej przy kącie 30
b − długość przyprostokątnej przy kącie 60
c − długość przeciwprostokątnej
Z układu równań:
2 = a + b − c
Po rachunkach wychodzi:
a = 3 +
√3
b =
√3 + 1
c = 2(
√3 + 1)
29 kwi 09:07
K+K: ja zrobiłam z zależności w trójkącie 30,60,90,stopni ale wyszło mi to samo
29 kwi 09:22
kamis:
3.
|Ω| = 2
3 = 8
A − zdarzenie polegające na wyrzuceniu co najmniej dwukrotnie orła
|Ω| = 6
2 = 36
B − zdarzenie polegające na wypadnięciu dwukrotnie parzystej liczby oczek
| | 1 | | 1 | |
Podstawiając do W(x) odpowiednio w miejsce x = |
| i x = |
| mamy: |
| | 2 | | 4 | |
1 = a + 2b
1 = a+ 4b
Z tego otrzymujemy:
a = 1
b= 0
W(x) = 8x
3 − 6x
2 + x = x(8x
2 − 6x + 1)
Trzecim pierwiastkiem wielomianu jest x = 0
29 kwi 09:27
K+K: kamis a jakbym chciała zrobić zdarzenie odwrotne do zdarzenia a to jak by to byo
29 kwi 09:34
Rivi: To wtedy kiedy orzeł wypada raz lub wcale jest zdarzeniem odwrotnym. Generalnie przy takim
zadaniu, to najlepiej wypisać wszystkie (całe osiem) i wybrać te pasujące

z którym masz
problem zadaniem?

29 kwi 09:54
K+K: wiesz nie bardzo wiem jak narysować zbiór A z zad 2
29 kwi 10:01
luk18: rysujesz prostą x=−1 i x=3 i zamalowywujesz przestrzeń między nimi. A skąd masz ten arkusz bo
robiłem kiedys chyba taki sam....
29 kwi 10:06
Rivi: Rysujesz dwie proste x=−1 i x=3 − pomiędzy nimi jest interesujące nas pole. To "iksy" mamy
| | 1 | | 1 | |
Rysujesz dwie proste y=− |
| x−2 oraz y=− |
| x+1 I pole pomiędzy tymi czterema prostymi |
| | 2 | | 2 | |
| | | |
jest interesującym nas zbiorem.  |
| |
| | | |
masz może odp do zad.9? Chciałbym zobaczyć czy dobrze zrobiłem

29 kwi 10:08
K+K: babka od matmy dała
29 kwi 10:08
Rivi: Zadanie drugie było w maju2009

29 kwi 10:10
K+K: zaraz wrzucę
29 kwi 10:10
29 kwi 10:16
Rivi: Dziękuje

29 kwi 10:22
kamis: 6.
Pole pierścienia: πr
12 − πr
22 = π(r
12 − r
22)
Jeśli połączysz punkty A i B cięciwy ze środkiem okręgów, przyjmijmy punktem S to w wyniku tego
powstanie trójkąt równoramienny, o ramionach długości promienia okręgu r
1, podstawie długości
cięciwy AB i wysokości opuszczonej na podstawę długości promienia okręgu r
2.
Przyjmijmy punkt D, za punkt styczności r
2 z cięciwą
Z trójkąta prostokątnego ADS i z tw. Pitagorasa:
| | AB2 | |
Podstawiając do pola pierścienia: π(r12 − r22) = π |
| |
| | 4 | |
29 kwi 10:31
K+K: dzięki
kamis 
29 kwi 10:39
luk18: | | 2√105 | |
ale tyle ci wyszedł sinα ? Czy takie są odpowiedz? Bo m wyszedł |
| |
| | 15 | |
29 kwi 10:39
Rivi: | | √15 | | a√3 | |
Wyszedł mi tyle, musisz gdzieś mieć błąd. hśb= |
| 1/3hp= |
| z pitagorasa H |
| | 2 | | 6 | |
29 kwi 10:42
Rivi: | | √15 | | a√3 | |
Wyszedł mi tyle, musisz gdzieś mieć błąd. hśb= |
| 1/3hp= |
| z pitagorasa H |
| | 2 | | 6 | |
29 kwi 10:43
Rivi: hśboczywiście też z "a" na końcu
29 kwi 10:43
K+K: takie są odp bo patrz
przyjmijmy że h to wysokość podstawy
H to wysokość ostrosłupa
a krawędź podstawy
2a krawędź boczna
h=U{a
√3}{2]
i z twierdzenia pitagorasa (ściana boczna)
| | 1 | |
dalej z twierdzenia pit (trójkąt z h i H i |
| h) |
| | 3 | |
| | a√33 | | a√15 | |
stąd sinα= |
| : |
| |
| | 3 | | 2 | |
| | 2√55 | |
odwracasz mnożysz i wychodzi ci sinα |
| |
| | 15 | |
29 kwi 10:51
Rivi: K+K, tylko na maturze nie przyjmuj, że wysokość ściany bocznej to "h" a 13h to podstawy.
Bo te "h" są różne, i by Ci odjęli. Najlepiej z indeksem hśb hp H, lub inna literkę niż te
same oznaczenie to czegoś różnego
29 kwi 10:52
K+K: no tak za szybko pisałam he

29 kwi 10:54
K+K: mógłby mi ktoś pomóc zadaniem 4 bo w ogóle nie mam pomysłu
29 kwi 10:56
Rivi:

| | | |
Czwarte jest beznadziejne  |
| |
| | | |
| | | |
Skoro [BC]=[6,2] to [AD]=[6,2] |
| |
| | | |
| | | |
a=(x,y) S=(0,0) [AS]=[3,1] |
| |
| | | |
| | | |
d=a+[AD](−3+6,−1+2) d=(3,1) |
| |
| | | |
29 kwi 11:05
K+K: no i proste a ja się tak głowiłam

29 kwi 11:18
K+K: ten wielomian w zadaniu 11 jest do potęgi 2005 ale i tak nie wiem jak się za nie zabrać

29 kwi 11:23
Artur: ja mam pytanie do 10 zadania, jak mamy |x2 + y2|≤9 to nie potrzeba tego rozpisywać na jakieś
dwa przypadki, bo wartość bezwzględna z liczby podniesionej do kwadratu jest dodatnia, prawda?
29 kwi 11:33
K+K: tak
29 kwi 11:36
K+K: tylko wiesz w tym drugim zbiorze y powinien być bez wartości bezwzględnej bo jakieś dziwadło
wyjdzie
29 kwi 11:39
Vax: Aby obliczyć sumę współczynników wielomianu należy policzyć jego wartość dla x=1
29 kwi 11:50
K+K: miłego rozwiązywania

ja muszę już uciekać na zakończenie roku


29 kwi 11:56
Żarliwy: W zadaniu ostatnim podstawiasz jedyneczkę za xsa. Wiesz dlaczego

? I mamy (−1)
2005, a to jest
równe −1.
29 kwi 13:58
;): 1 Wyznacz wszystkie wartości parametru m , dla których równanie x2 + mx + 8 = 0 ma dwa różne
pierwiastki rzeczywiste takie, że suma ich kwadratów jest równa 11m − 34 .
Δ > 0
x12 + x22 = 11m − 34 (x1 + x2)2 − 2x1x2 = 11m − 34
Δ = m2 − 32
(m + 4√2)(m − 4√2) > 0 ⇒ m∊(−∞,−4√2)∪(4√2,∞)
m2 − 16 = 11m − 34
m2 − 11m + 18 = 0
Δ = 121 − 72
√Δ = 7
m1 = 2 m2 = 9 ⋀ m∊(−∞,−4√2)∪(4√2,∞) ⇒ m = 9
29 kwi 16:55
;):
2 Funkcja liniowa f określona jest wzorem f(x) = ax + b dla x ∈ R .
a) Dla a = 2008 i b = 2009 zbadaj, czy do wykresu tej funkcji należy punkt P = (2009,2009
2) .
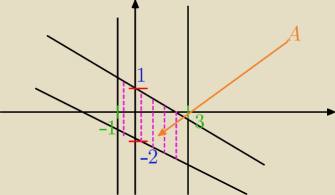
b) Narysuj w układzie współrzędnych zbiór
| | 1 | |
A ={ (x,y) : x ∈ <− 1,3> i y = − |
| x + b i b ∈ <− 2,1>} |
| | 2 | |
a)
f(x) = 2008x + 2009 P∊ f(x) ⇒ 2009
2 = 2009(2008 + 1) 2009
2 = 2009
2
29 kwi 17:06
;): 3. Dany jest wielomian W (x) = 8x
3 − 6x
2 + ax + b . Jednym pierwiastkiem wielomianu jest
prawdopodobieństwo otrzymania co najmniej 2 razy orła w trzykrotnym rzucie monetą. Drugi
pierwiastek jest równy prawdopodobieństwu wypadnięcia parzystej liczby oczek na każdej kostce
w rzucie dwiema kostkami. Wyznacz trzeci pierwiastek wielomianu
Ω
= = 2
3 = 8
A = {(O,O,R),(O,R,O),(R,O,O),(O,O,O)} A
= = 4
Ω
= = 36
B = {(2,2),(2,4),(4,2),(2,6),(6,2),(4,4),(4,6),(6,4),(6,6)} B
= = 9
| | 1 | | 3 | | 1 | |
W( |
| ) = 0 ⇒ 1 − |
| + |
| a + b = 0 |
| | 2 | | 2 | | 2 | |
| | 1 | | 1 | | 3 | | 1 | |
W( |
| ) = 0 ⇒ |
| − |
| + |
| a + b = 0 |
| | 4 | | 8 | | 8 | | 4 | |
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
a = 1 b = 0
W(x) = 8x
3 − 6x
2 + x ⇒x
3 = 0
29 kwi 17:20
Tomek.Noah: ok jakby ktos chcail to zrobilem wszystkie zadania

29 kwi 18:02
;):
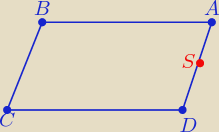
4. Punkt S = (0 ;0) jest środkiem boku AD równoległoboku ABCD . Wiadomo też, że AB
→ = [4;3]
oraz BC
→ = [6;2] . Wyznacz wierzchołki tego równoległoboku.
AD
→ = BC
→
[−x,−y] = [3,1]
A = (−3,−1)
D = (3,1)
B = (1,2)
C = (7,4)
29 kwi 18:07
;): 5. Ciąg (a,b,c) jest geometryczny i a + b + c = 2 6 , zaś ciąg (a− 5,b− 4,c− 11) jest
arytmetyczny. Oblicz a,b,c .
b2 = ac
2b − 8 = a + c − 16⇒ 2b + 8 = a + c
a + b + c = 26 ⇒3b = 18 b = 6
c = 20 − a
a2 − 20a + 36 = 0
Δ = 100 − 36
√Δ = 8
a1 = 10 − 8 = 2 a2 = 10 + 8 = 18
c1 = 18 c2 = 2
29 kwi 18:14
;):
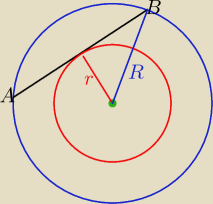
6. Dany jest okrąg O
1 . Kreślimy cięciwę AB nieprzechodzącą przez środek okręgu O
1 , a
następnie rysujemy okrąg O
2 współśrodkowy z okręgiem O
1 i styczny do cięciwy AB . Okręgi O
1
i O
2 ograniczają pierścień kołowy. Uzasadnij, że pole pierścienia kołowego nie zależy od
długości promienia okręgu O
1 (zależy tylko od długości cięciwy AB ).
R − promień dużego koła
r − promień małego koła
P
pierścienia = π(R
2 − r
2)
| | 1 | |
Ppierścienia = π( |
| |AB|) |
| | 4 | |
Więc pole pierścienia zależy od długości cięciwy AB c.n.u
29 kwi 18:24
;):
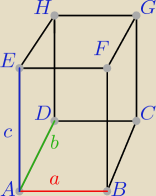
7. Długości trzech krawędzi prostopadłościanu wychodzących z jednego wierzchołka tworzą ciąg
geometryczny o sumie 19. Objętość prostopadłościanu jest równa 216. Wyznacz pole powierzchni
całkowitej tego prostopadłościanu.
a∊(0,13)
a + b + c = 19 ⇒ c = 13 − a
abc = 216 ⇒ b
3 = 216 b = 6
b
2 = ac
a
2 − 13a + 36 = 0
Δ = 169 − 144
√Δ = 5
a
1 = 4 a
2 = 9
c
1 = 9 c
2 = 4
P
c = 2 (4 * 6 + 4 * 9 + 6 * 9) = 228[j]
2
29 kwi 18:42
Jakub: Bardzo łatwe.
29 kwi 18:46
;):
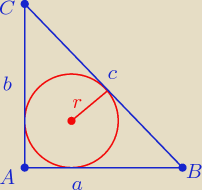
8. Jeden z kątów trójkąta prostokątnego ma miarę 60
o , promień okręgu wpisanego w ten trójkąt
ma długość 1. Oblicz długości boków trójkąta.
a + b − c = 2
c = 2(
√3 + 1)
b = 3 +
√3
a =
√3 + 1
29 kwi 19:08
;): Oczywiście zapomniałem kątów przy rysunku
29 kwi 19:09
dawid: oblicz pole powierzchni i objetosc stożka ,którego tworząca wynosi 5cm a promień podstawy jest
równy 3cm
29 kwi 20:15
Rivi: dobrze narysowałem te zbiory w 8.?
| | | |
Czyli AnB to jest to małe kółko w środku (niebieskozielone) a AnB' to jest pierścień? |
| |
| | | |
wiem, jakoś obrazka powala

30 kwi 15:17
Rivi: przepraszam, w 10

30 kwi 15:23
30 kwi 15:25
Rivi: Ach... czyli oryginalnie tam nie ma wart. bezwzględnej? Aaaacha...

30 kwi 15:41
ceaser I: macie gdzieś do tego gotowe odpowiedzi, bardzo bym prosił

30 kwi 15:44
 zad.1.
Wyznacz wszystkie wartości parametru m , dla których równanie x2 + mx + 8 = 0 ma dwa różne
pierwiastki rzeczywiste takie, że suma ich kwadratów jest równa 11m − 34 .
Zad.2.
Funkcja liniowa f określona jest wzorem f(x) = ax + b dla x ∈ R .
a) Dla a = 2008 i b = 2009 zbadaj, czy do wykresu tej funkcji należy punkt P =
(2009,20092) .
b) Narysuj w układzie współrzędnych zbiór
zad.1.
Wyznacz wszystkie wartości parametru m , dla których równanie x2 + mx + 8 = 0 ma dwa różne
pierwiastki rzeczywiste takie, że suma ich kwadratów jest równa 11m − 34 .
Zad.2.
Funkcja liniowa f określona jest wzorem f(x) = ax + b dla x ∈ R .
a) Dla a = 2008 i b = 2009 zbadaj, czy do wykresu tej funkcji należy punkt P =
(2009,20092) .
b) Narysuj w układzie współrzędnych zbiór

 z którym masz
problem zadaniem?
z którym masz
problem zadaniem? 










 ja muszę już uciekać na zakończenie roku
ja muszę już uciekać na zakończenie roku 

 ? I mamy (−1)2005, a to jest
równe −1.
? I mamy (−1)2005, a to jest
równe −1.
 2 Funkcja liniowa f określona jest wzorem f(x) = ax + b dla x ∈ R .
a) Dla a = 2008 i b = 2009 zbadaj, czy do wykresu tej funkcji należy punkt P = (2009,20092) .
b) Narysuj w układzie współrzędnych zbiór
2 Funkcja liniowa f określona jest wzorem f(x) = ax + b dla x ∈ R .
a) Dla a = 2008 i b = 2009 zbadaj, czy do wykresu tej funkcji należy punkt P = (2009,20092) .
b) Narysuj w układzie współrzędnych zbiór

 4. Punkt S = (0 ;0) jest środkiem boku AD równoległoboku ABCD . Wiadomo też, że AB→ = [4;3]
oraz BC→ = [6;2] . Wyznacz wierzchołki tego równoległoboku.
AD→ = BC→
4. Punkt S = (0 ;0) jest środkiem boku AD równoległoboku ABCD . Wiadomo też, że AB→ = [4;3]
oraz BC→ = [6;2] . Wyznacz wierzchołki tego równoległoboku.
AD→ = BC→
 6. Dany jest okrąg O1 . Kreślimy cięciwę AB nieprzechodzącą przez środek okręgu O1 , a
następnie rysujemy okrąg O2 współśrodkowy z okręgiem O1 i styczny do cięciwy AB . Okręgi O1
i O2 ograniczają pierścień kołowy. Uzasadnij, że pole pierścienia kołowego nie zależy od
długości promienia okręgu O1 (zależy tylko od długości cięciwy AB ).
R − promień dużego koła
r − promień małego koła
Ppierścienia = π(R2 − r2)
6. Dany jest okrąg O1 . Kreślimy cięciwę AB nieprzechodzącą przez środek okręgu O1 , a
następnie rysujemy okrąg O2 współśrodkowy z okręgiem O1 i styczny do cięciwy AB . Okręgi O1
i O2 ograniczają pierścień kołowy. Uzasadnij, że pole pierścienia kołowego nie zależy od
długości promienia okręgu O1 (zależy tylko od długości cięciwy AB ).
R − promień dużego koła
r − promień małego koła
Ppierścienia = π(R2 − r2)
 7. Długości trzech krawędzi prostopadłościanu wychodzących z jednego wierzchołka tworzą ciąg
geometryczny o sumie 19. Objętość prostopadłościanu jest równa 216. Wyznacz pole powierzchni
całkowitej tego prostopadłościanu.
a∊(0,13)
a + b + c = 19 ⇒ c = 13 − a
abc = 216 ⇒ b3 = 216 b = 6
b2 = ac
a2 − 13a + 36 = 0
Δ = 169 − 144
√Δ = 5
a1 = 4 a2 = 9
c1 = 9 c2 = 4
Pc = 2 (4 * 6 + 4 * 9 + 6 * 9) = 228[j]2
7. Długości trzech krawędzi prostopadłościanu wychodzących z jednego wierzchołka tworzą ciąg
geometryczny o sumie 19. Objętość prostopadłościanu jest równa 216. Wyznacz pole powierzchni
całkowitej tego prostopadłościanu.
a∊(0,13)
a + b + c = 19 ⇒ c = 13 − a
abc = 216 ⇒ b3 = 216 b = 6
b2 = ac
a2 − 13a + 36 = 0
Δ = 169 − 144
√Δ = 5
a1 = 4 a2 = 9
c1 = 9 c2 = 4
Pc = 2 (4 * 6 + 4 * 9 + 6 * 9) = 228[j]2
 8. Jeden z kątów trójkąta prostokątnego ma miarę 60o , promień okręgu wpisanego w ten trójkąt
ma długość 1. Oblicz długości boków trójkąta.
8. Jeden z kątów trójkąta prostokątnego ma miarę 60o , promień okręgu wpisanego w ten trójkąt
ma długość 1. Oblicz długości boków trójkąta.


 http://www.zadania.info/5766460
http://www.zadania.info/5766460

