t MARTA: Jak rozwiązać tą nierówność?

	1
sin 2x < −		x ∊ < 0, 2π>
	2

małgosia: naszkicuj sobie wykres funkcji sin2x i zobacz w których miejscach wartości będa mniejsze niz −1/2 ; punkty przecięcia wyznaczysz rowiązując równanie sin2x = − 1/2

MARTA: no własnie mi nie wychodzi bo mam podane przedziały.... dwa.. i nie wiem dlaczego tak..

bart: x_o=−30^o +2k*180^o u x_o=−150^o +2k*180^o mamy 2x wiec: x=−15+k*180^o u x=−75^o+k*180^o

bart:

	π		5π
czyli x∊(		+kπ ;		+k*π) gdzie k to calkowita liczba
	12		12

bart: minusy oczywiscie przed tymi wartosciami,, sorry

MARTA: hmm a w odp mam tak :

	7π		11π		19π		23π
x ∊ (		,		) ∪ (		,		)
	12		12		12		12

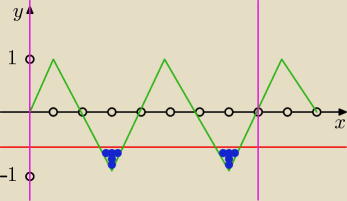
małgosia: no to jeśli masz podany przedział od 0 do 2π to tym łatwiej. rysujesz wtedy wykresik tylko dla tego przedziału

	π
każda kropka to
	4

MARTA: mmm to ja zle wykres narysowałam i dlatego... dziękuję bardzo

Maryjusz: Narysuj sobie sinx.

	1		7π		11π
W przedziale <0; 2π> sinx jest mniejszy od −		w przedziale (		;		)
	2		6		6

Teraz zauważ, że masz 2x, więc:

	7π		11π
2x =		+2kπ v 2x =		+2kπ /:2
	6		6

	7π		11π
x=		+kπ v x =		+kπ
	12		12

Podstawiam za k:

	7π		11π
k=0 ⇔ x ∊ (		;		)
	12		12

	19π		23π
k=1 ⇔ x ∊ (		;		)
	12		12

Dla k=2 x nie należy już do przedziału.

MARTA: dziękuje