planimetria
K+K: W trójkącie ABC punkt S jest środkiem okręgu wpisanego, a punkty KLM są punktami styczności
okręgu wpisanego w trójkąt z bokami BC ,CA i AB odpowiednio.
* Uzasadnij, że na czworokącie AMSL można opisać okrąg.
* Wiedząc, że |∡CAB | = 38st oraz |∡ABC | = 58st oblicz miary kątów trójkąta KLM .
28 kwi 19:12
K+K: podbijam
28 kwi 19:37
K+K: pobijam
28 kwi 19:56
Mamba: a nie ma nic powiedziane, że to równoboczny?

28 kwi 19:58
K+K: nie
28 kwi 19:59
K+K: pomoże ktoś

28 kwi 20:12
Mamba: aby dało się wpisać to musi byc spełniony warunek |AL|+|SM|=|MA|+|SL|
|SL|=|SM|, bo to promień koła wpisanego w trójkąt ABC
zostaje |AL|=|MA| no i to tyle co wymyśliłam, jeśli to cokolwiek Ci pomoże
28 kwi 20:13
K+K: czyli wychodziłoby że można opisać na nim okrąg
28 kwi 20:20
K+K:
to będzie tak
Jeżeli połączymy środek okręgu wpisanego S z punktami styczności K ,L,M to odcinki SK ,SL,SM
są prostopadłe do odpowiednich boków. W takim razie dwa przeciwległe kąty SLA i SMA
czworokąta AMSL są proste, czyli na czworokącie tym można opisać okrąg (co więcej średnicą
tego okręgu jest AS ).
28 kwi 20:25
Eta:
1/
ΔAMS przystaje do Δ ALS
miara kąta MBL= 142
o
W czworokącie AMSL sumy kątów przeciwległych mają miary :
90
o+90
o = 38
o + 142
o =
180o − to warunek wpisania czworokąta w okrąg
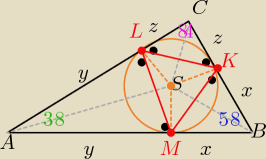
2/ trójkąty: AML , BMK , KLC są równoramienne
wyznacz miary kątów przy ramionach : y, x , z
zatem |<K| = 180
o −( 48
o + 61
o) =..........
|< M | = 180
o −( 61
o +71
o)=......
|<L | = 180
o −(71
o + 48
o)=.......
28 kwi 20:25
K+K: dzięki też już doszłam

28 kwi 20:33
K+K: eta mogłabyś pomóc Asi

28 kwi 20:34


 1/
ΔAMS przystaje do Δ ALS
miara kąta MBL= 142o
W czworokącie AMSL sumy kątów przeciwległych mają miary :
90o+90o = 38o + 142o = 180o − to warunek wpisania czworokąta w okrąg
2/ trójkąty: AML , BMK , KLC są równoramienne
wyznacz miary kątów przy ramionach : y, x , z
zatem |<K| = 180o −( 48o + 61o) =..........
|< M | = 180o −( 61o +71o)=......
|<L | = 180o −(71o + 48o)=.......
1/
ΔAMS przystaje do Δ ALS
miara kąta MBL= 142o
W czworokącie AMSL sumy kątów przeciwległych mają miary :
90o+90o = 38o + 142o = 180o − to warunek wpisania czworokąta w okrąg
2/ trójkąty: AML , BMK , KLC są równoramienne
wyznacz miary kątów przy ramionach : y, x , z
zatem |<K| = 180o −( 48o + 61o) =..........
|< M | = 180o −( 61o +71o)=......
|<L | = 180o −(71o + 48o)=.......

