Prosze o rozwiązanie poniższego zadania, jeśli to możliwe: sprd123: Witam! Prosze o rozwiązanie poniższego zadania, jeśli to możliwe: Pole trójkąta ABC = 27cm Oblicz długość boku BC tego trójkąta, wiedząc że: |AB| = 6, |AC| = 10, i że kąt między nimi jest ostry. Prosze o dokładnie rozpisanie co i jak, gdyż jutro mam sprawdzian a jestem zielony póki co. Pozdrawiam!

sprd123: Nikt nic nie wie?

ICSP: Myślisz że w 7 minut już dostaniesz gotowe rozwiązanie?

K+K: masz odp do tego

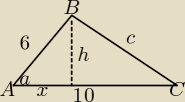
Kuba: Pole_ABC=1/2*60*sina 27==1/2*60*sina sina=27/30 cos²a=1−729/900 cos²a=171/900 cosa=√171/30 c²=100+36−120*√171/30 c²=136−4√171 c=√136−4√171=2√34−√171

Rivi:

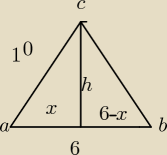
1. h ze wzoru na pole trójkąta

2. x z pitagorasa

3. 6−x=?

4. Szukany bok BC z pitagorasa

sprd123: ok dziękuje. A możesz mi jeszcze napisać co i jak tutaj jest? a mianowicie: Pole ABC = 1/2 x 60 x sin a − dlaczego x 60 i x sina ? cos²a = 1−729/900 − dlaczego i co to jest wgl.? I to poniżej to już wgl. magia.

ICSP: POdstawy rozszerzenia. Twierdzenie cosinusów a wcześniej wzór na pole trókąta: P = U{1]{2}absinα gdzie α jest kątem zawartym między bokami ab.

Rivi: Kuba, masz dobrze, dobry wynik, taki jak u mnie, ale chyba jednak mój sposób łatwiejszy dla niego

sprd123: Rivi a mógłbys to mi rozpisać?

Kuba: no fakt twój sposób jest lepszy :S

Rivi:

1. P=12*a*h=12*6*h=27 h=9

2.x2=102−92=19 x=√19

3. 6−x=6−√19

4. IBCI2=92+(6−√19)2=81+36−12√19+19=136−12√19

IBCI=√136−12√19=2√34−3√19

Rivi:

1. P=12*a*h=12*6*h=27 h=9

2.x2=102−92=19 x=√19

3. 6−x=6−√19

4. IBCI2=92+(6−√19)2=81+36−12√19+19=136−12√19

IBCI=√136−12√19=2√34−3√19

Rivi:

1. P=12*a*h=12*6*h=27 h=9

2.x2=102−92=19 x=√19

3. 6−x=6−√19

4. IBCI2=92+(6−√19)2=81+36−12√19+19=136−12√19

IBCI=√136−12√19=2√34−3√19

sprd123: ale jednak inne rozwiązanie niż u Kuby?

Rivi: To samo, √171=3√19

Kuba: bo ja nie wyciągnąłem pierwiasstka 9*19=171 czyli tak jak u mnie

sprd123: ahaaa. Dziękuje Wam bardzo. Mam nadzieję, że jutro dam sobię z tym radę.

sprd123: Jeszcz nie kumam jednego. W drugim punkcie jak Ty to policzyles ze wzoru pitagorasa? Przecież wzór jest a²+b²=c² ?

Rivi: a²+b²=c² a²=c²−b²

sprd123: dobra już kumam. To poprostu przekształcenie. Debil ze mnie xD

sprd123: Słuchaj, a nie powinno tam być 81+36+12{19}? Bo masz tam minus 12{19} a nie powinno byc plus? Bo wg. wzoru skróconego mnozenia: (a−b)² = a² − 2ab + b² a więc: |BC|² = (6− √19)² +9² = 81 + 36 −2(−6√19) +36 = 81 +36 + 12√19 + 19= 136 + 12{19} ?

Rivi: nie, nie, nie. a=6 b=√19, bez minusa. Tak mógłbyś podstawiać do (a+b)², gdzie a=6 b=−√19

sprd123: aha rozumiem . No widzicee, ja cienki jestem