Wyznacz dziedzinę funkcji f(x)=log(x^{3}-7x^2+6)- log(25-x^2) Tomek: Wyznacz dziedzinę funkcji f(x)=log(x³−7x²+6)− log(25−x²) skorzystałem z własności logarytmów i zapisałem równanie (x³−7x²+6)/(25−x²)>0 i wyliczyłem pierwiastki a w rozwiązaniach pisze że trzeba rozpatrywać osobno (x³−7x²+6)>0 i (25−x²)>0 i wyznaczyć część wspólną i teraz pytanie czemu tak a nie tak jak ja to zrobiłem? z góry dzięki za odpowiedź

saus: Aby wyznaczyć dziedzinę funkcji f(x), musisz zwrócić uwagę na to, że: 1) x³ − 7x² + 6 > 0 2) 25 − x² > 0 3) (x³ − 7x² +6) : (25 − x²) > 0 i 25 − x² nie może być zerem, pozdrawiam.

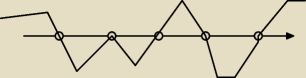
Tomek: liczby w kolejności od lewej to −5 ; 3−√15 ; 1 ; 5 ; 3+√15 powiedzcie mi czy dobrze narysowałem ten wykres (co prawda arcydziełem nie jest ale chyba czytelny?) a na rysunku narysowałem tą nierówność oczywiście z tego zadania (x²−6x−6)(x−1)(x+5)(x−5)>0

saus: jeśli masz (x³−7x²+6)(5−x)(x+5) > 0 to zaczynasz od prawej strony i ciągniesz krzywą od dołu, bo masz w iloczynie 5−x

saus: ponadto każdy pierwiastek jest jednokrotny, więc bez odbić od osi x

Tomek: hmm to kiedy w końcu są odbicia?

;): saus jak dajesz warunek 25 − x² > 0 to od razu z niego wynika że nie może on być zerem

Tomek: aha no to wielkie dzięki za pomoc a tak na przyszłość w innych przykładach to kiedy sie odbija? bo wiem jak jest kwadrat ale nie wiem przy jakim pierwiastku sie odbija

;): Kiedy pierwiastek wielomianu jest 2n czyli po prostu parzysty 2,4,6 itd wtedy odbijasz od osi OX

saus: "" Podałem tylko wszystkie założenia, które należy przyjąć. To że w syntezie wychodzi co wychodzi to inna bajka. Radzę postępować ostrożnie z zapisami i skrótami i robić powoli i po kolei. Można narobić błędów i nie trafić w klucz.

Tomek: oki dzięki postaram się