wartość bezwględna orange91: wartość bezwzględna Proszę o pomoc: |x+2√3−|3−2√3||=1

Rivi: 3−2√3 jest ujemna więc zmieniasz znak przy znikaniu bezwzględnej Ix+2√3+3−2√3I=1 Ix+3I=1 już chyba dasz radę

Mati: x+2√3 +3 − 2√2 = 1 lub x+2√3 +3 − 2√2 = −1

Mati: oj tak, pomyłka, kolega na górze dobrze zrobił

orange91: Dzięki no to teraz już wiem co mi nie pasowało ah te głupie błędy.

bachus: Ja robię z wartością bezwzględną tak jak Mati. Mniej roboty

bachus: kurde, jak mamy |x+3|+|x+1|=x+18 D (−3,−1) x+3+x+1=x+18 2x+4=x+18 2x=x+14 x=7

K+K: co Ty zrobiłeś z tym równaniem

bachus: mów co jest źle

Rivi: Tak, można jak Mati... tylko że tu masz dwie wartości bezwzględne, i najpierw opuszczasz tą w środku

Mati: To wkoncu moje jest poprawne czy nie?

K+K: bachus a czy nie trzeba tego rozpatrywać w przedziałach

bachus: rozpisz to proszę bo już nie wyrabiam z równaniami z wartościami bezwzględnymi mamy taką równość i co dalej.... |x+3|+|x+1|=x+18

Rivi: Mati, w sumie nie. Trzeba najpierw usunąć tą wartość ze środka. Zostaje Ix+3I=1

i rozbijamy

x+3=1 x=−2 i x+3=−1 x=−4

Mati: Ok, dzięki za objaśnienie |x+3|+|x+1|=x+18 To bym rozpatrywał na 3 przedziałach... (−∞, −3), <−3, −1>, (−1, +∞)

Mati: (−∞, −3>, (−3, −1), <−1, +∞) ewentualnie chyba bardziej takim.

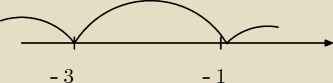
K+K: x= −3 x= −1 i wychodzą przedziały takie i dla każdego inaczej opuszczasz znaki w wartościach zacznij od przedziału x∊(−∞; −3) −x−3−x−1=x+18 i sprawdzasz czy rozwiązanie należy do tego przedziału i tak następne

Rivi: tak, ten przykład robi się jak mówisz

K+K: uff to dobrze może nie jest ze mną aż tak źle

bachus: a nie jest tam taki przedział (−3,−1>?

Rivi: tak na prawdę nie ma znaczenia jak się zapisze przedział − nie ma wpływu na wynik.

K+K: to zależy gdzie domkniesz przedział a gdzie otworzysz jak ja napisałam (−∞; −3) to w następnym domknęłam <−3; −1)

Rivi: K+K, to akurat do Matiego było Już się pogubiłem... bo tu chyba dwa przykłady się przeplatają Jak robisz "falkę" to przy pojedynczych pierwiastkach ona przechodzi przez oś, nie odbija się

bachus: nie tylko zgodny wynik jest ważny w zadaniach otwartych

Rivi: tia, zależy od sprawdzającego... no ale fakt faktem, że to, czy domknie się go na końcu przedziału, czy na początku następnego nie ma znaczenia... bo w obu wariantach przy tym "iksie" wartość bezwzględna jest 0. No a 0=−0

K+K: no jeśli rozwiązanie nie będzie należało w jednym przedziale to będzie należało w drugim gdzie domkniesz

madzia: czyli z wszystkimi równośćiami/nierównościami z wartościami bezwzględnymi się robi w ten sposób? jakbym miała równość |x+2|>|x−1| to przedziały są (−∞,−2> (−2,1> <1,∞) czy inaczej?

K+K: tak mi się wydaje