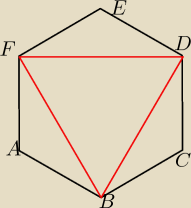
ZAD krucz: Bok sześciokąta foremnego ABCDEF ma długość 6 cm. Oblicz promień koła wpisanego w trójkąt BDFedcbaf

Vax: Niech d będzie długością boku trójkąta BDF, zauważ, że jest on równoboczny, policzysz jego

	a√3
długość boku z tw. kosinusów a potem skorzystaj ze wzoru r =
	6

Pozdrawiam.

ICSP: a ja sądze ze jest to krótsza przekątna sześciokąta foremnego dana wzorem d = a√3

Vax: Jest wiele sposobów, nie ma znaczenia z którego skorzystamy

ICSP: tylko że to zadanie z podstawy jest a na podstawie wątpię aby było twierdzenie cosinusów.

Vax: Z tymże osobiście nie polecam wkuwania wzorów, zdecydowanie lepsze jest rozumienie skąd one się biorą, jeżeli się to rozumie można nie korzystać z twierdzenia kosinusów tylko opuścić wysokość na przekątną BD z punktu C i skorzystać z własności trójkąta o kątach 30,60,90 czego uczą w gimnazjach.

krucz: ICSP ma racje nie brałem twierdzenia cosinusów

Vax: To posłuż się tym co napisałem przed chwilą.