które wyrazy ciągu an są ujemne, jeśli: ollaa: Pytanie. które wyrazy ciągu an są ujemne, jeśli: a) an= n−6/n+3 i robię tak: n−6/n+3<0 czyli (n−6)(n+3)<0 n−6<0 n+3>0 n<6 n>−3 odp. wyrazy ujemne to : a1,a2,a3,a4,a5 i to jest dobra odpowiedz natomiast w przykładzie: an=9−n/7−3n robię dokładnie to samo (9−n)<0 i (7−3n)>0 odpowiedz wychodzi zła . Natomiast gdy ułułoże równanie (9−n)>0 i (7−3n)<0 odpowiedz jest dobra. Czy mógłby mi ktoś wytłumaczyć jak to jest z tymi znakami ? BŁAGAM

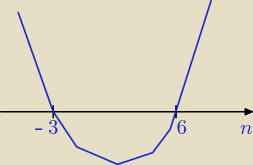
Vizer: Tak tego się nie robi rysujesz sobie wykres z boku i odczytuje( na gorze podam Ci przykład do pierwszego podanego przez Ciebie przykładu) czyli n∊(−3,6) ∧ n∊N₊ więc n∊{1,2,3,4,5} To samo robisz z podobnymi przykładami.

ollaa: dziękuję i jeszcze jedno pytanko od czego zależy czy ramiona paraboli są skierowane w górę?

Vizer: Od współczynnika a przy x² jeśli jest on dodatni to ramiona paraboli są skierowane do góry, a jeśli jest on ujemny to ramiona są skierowane do dołu.

ollaa: a w zadaniu takim które wyrazy ciągu an są większe od liczby x an= (n−3) do kwadratu , x=5 po obliczeniu wychodzi n²−6n+4>0 licze delte i wychodzi n=3−√5 i n= 3+√5 i nie wiem co dalej.. sorki że tyle pytań zadaje ale jutro mam sprawdzian i chciałam w miare dobrze wypaść

Vizer: Układasz postać iloczynową z tych pierwiastków co wyliczyłaś i odczytujesz z wykresu tak samo jak podałem wyżej przedział uwzględniając, że muszą to być liczby naturalne dodatnie.

ollaa: ok dzięki wielkie

justyna: an=−n2+11n−24

justyna: an=(n2−2)(16−n2)/n+1

Eta: Jakie jest pytanie do tych zadań?

justyna: do pierwszego które wyrazy ciągu (an ) są ujemne

justyna: a drugie które wyrazy ciagu są równe zeru

znak: No to rozwiązujesz, co za problem? (1) a_n < 0 (2) a_n = 0

Eta: n∊N+ 1/ −n²+11n−24<0⇒ (n−3)(n−8)>0 a₁, a₂,a₉,a₁₀, ..... 2/ n∊N+ to n+1>0 zatem (n²−2)(n²−16)=0 i n∊N+ ⇒ n=4 a₄=0 =====

justyna: dziękuję

Eta: @justyna Na przyszłość załóż nowy post ( nie wyciągaj postów sprzed 10 lat

6latek: a_n=0

(n2−2)(16−n2)
	=0
n+1

a
	=0 gdy a=0 i b≠0 skoro n∊N to mianownik nigdy nie bedzie rowny 0
b

Przyrownujemy licznik do 0 (n²−2)(16−n²)=0 to n²−2=0 lub 16−n²=0 n²−2=0 to (n−√2)(n+√2=0 to n=√2 lub n=−√2 n∉N odpoadaja 16−n²=0 to (4−n)(4+n)=0 to n=4 lub n=−4 rozwiazanie to tylko n=4 bo 4∊N

6latek: Wczoraj napisalem ABC zeby sie zatrzymal Wiec Ciebie tez prosze zatrzymaj sie tutaj i nieprzekraczaj granicy W zaden sposob nie obrazam Cie ani nie ponizam .Chcesz zablokowac to blokuj . Jedz dobre posilki i nie pomijaj ich .