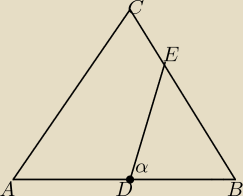
Prosta przechodząca przez środek jednego z boków trójkąta równobocznego i tworząca z nim kąt
ostry dzieli ten trójkąt na czworokąt i trójkąt. Stosunek pola czworokąta ADEC i trójkąta DBE
jest równy 5:3. Oblicz tangens kątaα.
| 5 | ||
stosunek pol: k2= | ||
| 3 |
| a2√3 | ||
PABC= | ||
| 4 |
| 1 | a2 | |||
PDBE= | * | *sin600 | ||
| 2 | 2 |
| 1 | a2 | |||
wolfy, skąd Ci się wzięło PDBE= | * | *sin600  | ||
| 2 | 2 |
dzięki za pomoc
sorki poddaje sie nie mam pojecia jak to ruszyc zostawie ci rysunek moze cos uda ci sie znalesc
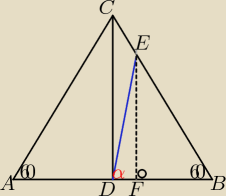Właśnie udało mi się to zrobić, a więc:
| a2√3 | ||
PΔABC= | ||
| 4 |
| 3 | 3a2√3 | 1 | a | 3a√3 | ||||||
Wiemy, że PΔDBE= | PΔABC= | = | * | *|EF| stąd |EF|= | ||||||
| 8 | 32 | 2 | 2 | 8 |
| a√3 | ||
Z ΔABC mam |CD|= | . Z podobieństwa ΔDBC i ΔFBE mamy: | |
| 2 |
| |EF| | |FB| | 3 | |||||||||
= | więc |FB|= | a | |||||||||
| |CD| |
| 8 |
| a | 3 | 1 | ||||
|DF|= | = | a= | a | |||
| 2 | 8 | 8 |
| |EF| | ||
tgα= | =3√3 | |
| |DF| |