funkcja kwadratowa Marek: Witam, Bardzo proszę o pomoc w rozwiązaniu zadań z matematyki − funkcja kwadratowa. Proszę o sposób rozwiązania + wyjaśnienia i wykresy, dlaczego powstał taki, a nie inny wynik. Przepraszam też za "opisowo−graficzną formę równań, ale nie mam zainstalowanego programu z równaniami. Zad.1 Wyznacz punkty przecięcia paraboli z osiami układu współrzędnych oraz współrzędne jej wierzchołka .Naszkicuj tę parabolę. y = − x2 + 2x + 3 „minus iks do potęgi drugiej plus dwa iks plus trzy” Zad.2 Rozwiąż układ równań i podaj jego interpretację geometryczną. { y = − x2 „minus iks do potęgi drugiej” { y = − x „minus iks” Zad.3 Przedstaw funkcję f w postaci iloczynowej. f (x) = 2x 2 + 2x – 4 „dwa iks do potęgi drugiej plus dwa iks minus cztery” Zad.4 Rozwiąż nierówność. X2 >/ 5 – 4x „ iks kwadrat większe lub równe od pięciu minus cztery iks” Zad.5 Naszkicuj wykres funkcji f . Wyznacz wartość najmniejszą i wartość największą funkcji f w podanym przedziale. f (x) = x2 + 2x + 1 , < 0; 2> „ iks kwadrat plus dwa iks plus jeden, przedział : <0 ; 2> Bardzo proszę Wszystkich o pomoc ! Pozdrawiam, Marek

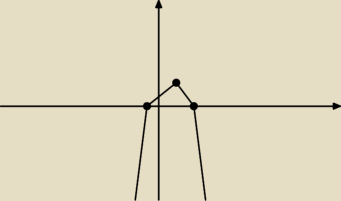DasAuto: Zad.1 y=−x²+2x+3 Obliczam miejsca zerowe funkcji ( gdzie przecina oś Ox) wyliczam delte : 4+12=16 pierwiastek z delty = 4

	−2−4
x1=		= 3
	−2

	−2+4
x2=		=−1
	−2

Wykres przecina oś Ox w punktach (3.0) i (−1,0) Wykres przecina oś Oy więc x=0 y=−0²+2*0+3=3 Przecina oś Oy w punkcie (0,3) Obliczam współrzędne wierzchołka

	b		2
p= −		= −		=1
	2a		−2

	16
q= −		= 4
	−4

Wierzchołek (1,4) Przepraszam za nie zbyt ładny rysunek

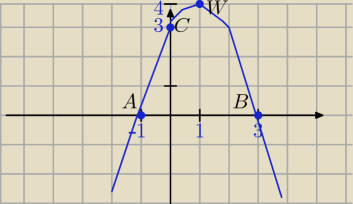Vizer: zad.1 Liczymy współrzędne wierzchołka paraboli

	−b		−2
xw=		=		=1
	2a		−2

y_w=f(x_w)= −1+2+3=4 W(1,4) Teraz liczymy współrzędne punktów przecięcia się z osiami. Zacznę od osi OX Liczymy deltę: Δ=4+12=16,√Δ=4

	−2−4		−6
x1=		=		=3
	−2		−2

	−2+4		2
x2=		=		=−1
	−2		−2

Punkty przecięcia sie osią OX: A(3,0), B(3,0) Liczymy teraz punkt przecięcia się z osią OY f(0)=3 C(0,3)

DasAuto: Zad.3 y=2x²+2x−4 Obliczamy deltę : 4+32=36 pierwiastek z delty = 6

	−2−6
x1=		= −2
	4

	−2+6
x2=		=1
	4

Zapisuje w postaci iloczynowej : y= a(x−x₁)(x−x₂) czyli y=2(x+2)(x−1)

sdcd: x−4