nierówności viktoria*************: Bardzo proszę o pomoc Rozwiązanie nierówności 1) 2x²+x−3<0 2) 2x³−1x²−8x+4>0

	x+3
3)		< 0
	3x−1

Proszę pomóżcie sama kompletnie nie wiem co robić,nie kumam tego

luk18: 1) wyliczasz deltę Δ=1−4*2*(−3)=1+24=25, √Δ=5. Teraz miejsca zerowe:

	−1−5		−6		−3
x1 =		=		=
	2*2		4		2

	−1+5		4
x2 =		=		=1
	2*2		4

Teraz robisz wykres, zaznaczasz na osi pierwiastki i rysujesz parabolę, potem sprawdzasz dla

	−3
jakich x parabola jest poniżej 0. w tym przypadku x∊(		;1)
	2

viktoria*************: Rozwiązanie nierówności 1) 2x2+x−3<0 2) 2x3−1x2−8x+4>0

	x+3
3)		< 0
	3x−1

Proszę pomóżcie sama kompletnie nie wiem co robić,nie kumam tego

luk18:

	p
2) korzystam z twierdzenia o pierwiastkach wymiernych
	q

3) ułamek ten zapisz jako iloczyn licznika i mianownika i tak samo jako podpunkt 1.

nick: z równania kwadratowego: 1) Δ= b² −4ac = 1+ 24 √Δ = 5 x₁ =.....itd wyjda ci 2 pierwiastki (miejsca zerowe) rysujesz os OX, zaznaczasz te dwa pierwiastki, jesli a>0 to ramiona do gory, jesli a<0 to ramiona w dół szukasz rozwiazan mniejszych od 0 wiec zaznaczasz to co nad osia, czyli rozw to (−∞, x₁) suma (x₂, +∞)

kachamacha: 1. Δ=1−4*2*(−3)=1+24=25

	−1+5
x1=		=1
	4

	−1−5		−3
x2=		=
	4		2

	−3
x∊(		,1)
	2

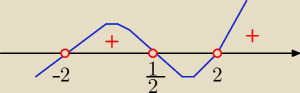
sowa: 2/ x²(2x−1) −4(2x−1) >0 (2x−1)(x²−4) >0 (2x−1)(x−2)(x+2) >0 x= ¹₂ v x= 2 v x= −2 x€ (−2, ¹₂) U ( 2,∞)

ICSP: co do trzeciego to przemnóż przez kwadrat mianownika po wcześniejszym ustaleniu dziedziny. Później rozwiąż nierówność kwadratowa. Pamiętaj o uwzględnieniu dziedziny.

sowa:

	1
3/ dla x ≠
	3

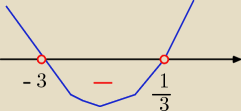
zamieniasz na iloczyn ( 3x−1)(x+3) <0 x₁= ¹₃ v x= −3 parabola ramionami do góry wartości ujemne są dla : x€ ( −3, ¹₃)

viktoria*************: Bardzo Wam dziękuję za pomoc

viktoria*************: Jestem bardzo wdzięczna

ICSP: Cieszymy się twoim szczęściem

viktoria*************: Pomocy Wcale nie umie nic z ciągów a muszę te zadania zrobić, mam to zadane do zaliczenia semestru. Liczę na Waszą pomoc. 1) Ciąg ( a_n) określony jest wzorem a_n=n²+20n+4 a) oblicz dziesiąty wyraz ciągu (a_n) b) o ile procent trzeci wyraz ciągu (a_n) jest większy od wyrazu drugiego? 2) Ciąg (a_n) określony jest wzorem a_n =−2n+5 a) uzasadnij ( na podstawie definicji), że ciąg (a_n) jest arytmetyczny b) suma ilu początkowych wyrazów ciągu (a_n) jest równa −14 c) określ monotoniczność ciągu (a_n). 3) Iloraz ciągu geometrycznego (a_n) równy jest 3, a suma odwrotności wyrazu pierwszego i drugiego wynosi 18 a) oblicz pierwszy wyraz ciągu (a_n) b) podaj wzór ogólny ciągu (a_n)

abc: 1 a) za n podstawiasz 10 i liczysz, mnożysz, dodajesz

	a3
b) za n podstawiasz 3, wyliczasz ile wynosi a3, to samo z a2, wtedy		*100%
	a2

abc: 2. z definicji jeśli a_n+1− a_n = r to ciąg jest arytmetyczny. r ma być liczbą. a_n+1 = −2(n+1)+5= −2n +3 a więc a_n+1− a_n = −2n+3 +2n − 5= −2 r=−2 c. arytmetyczny malejący

abc: 2c) juz w sumie wynika z a, ponieważ r=−2 to ciąg jest malejący

	1		1
3. q=3		+		= 18
	a1		a2

a₂=a₁*q, można podstawić i wyliczyć a₁

viktoria*************: tak prawdę mówiąc nic z tego nie rozumie