Zadania obowiązkowe aby dostać 2 z maty na koniec..
Rollnick: Te zadania musze zrobić aby dostać dopalacza na koniec.. robię je ale nie wiem czy dobrze

wiec proszę was o pomoc w rozwiązaniu tych zadań.

Z góry serdecznie dziękuję

1) Rozwiąż nierówność (muszą być wykresy)
a) x
2−5x+6>0
b) x
2<9x
1a) narysuj wykres funkcji y=x
2−5x+6 (x1,x2,w) Podaj postać kanoniczną i iloczynową
2)Rozwiąż równania
a) 2x
3−x
2+2x−1=0
b) 5x
3+2x
2−5x−2=0
c) 5x
3=25x
3)Znajdź Ymin, Ymax w przedziale <−1;2> jeśli y=x
2−x
4)Rozwiąż nierówność i równanie
a) |x−2|<3
b) |x+3|>/2 −> nie wiem jak się tu robi znak mniejsze bądź równe

c) |x+3|=5
5) Napisz równanie prostej prostopadłej i równoległej do y=3x+7 przechodzącej przez punkt
P=(−2;5)
6) Wyznacz równanie prostej jeśli f(−3)=4 i f(z)=−5
7) Rozwiąż równanie
8) Obl.
| | 1 | |
√sin2α−2cos2α jeśli tgα= |
| |
| | 2 | |
9)Obl m jeśli punkt P(−3;8) należy do wykresu funkcji f(x)=(3m−2)x+4m−2
Dla jakiego m funkcja jest rosnąca?
10)Obl x jeśli wyrazy tworzą x+1, 2x−3, 4−5x
a) ciąg arytmetyczny
b) ciąg geometryczny
11) Sprawdź czy ciąg an=3n−4 jest
a) arytmetyczny
b0 geometryczny
12) Napisz równanie okręgu o środku w S=(−3,4) i promieniu r=5
26 kwi 17:56
Kejt: dobra.. ja mogę się zaopiekować 1 i 2.. może znajdą się chętni na pozostałe..
26 kwi 17:57
Kejt:
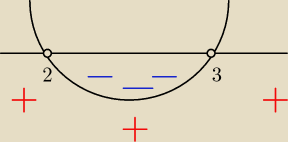
a) x
2−5x+6>0
Δ=25−6*4=25−24=1
√Δ=1
| | −(−5)−1 | | 5−1 | | 4 | |
x1= |
| = |
| = |
| =2 |
| | 2 | | 2 | | 2 | |
| | −(−5)+1 | | 5+1 | | 6 | |
x2= |
| = |
| = |
| =3 |
| | 2 | | 2 | | 2 | |
interesują nas wartości dodatnie, więc:
x∊(−
∞;2)∪(3;+
∞) (patrz: rysunek)
26 kwi 18:28
martuniaaa xD: zad 12
(x + 3)2 + (y − 4)2= 25
26 kwi 18:36
Kejt:
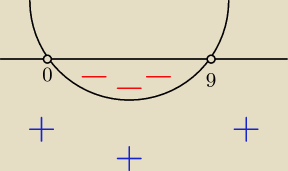
b) x
2<9x
x
2−9x<0
x(x−9)<0
x=0 v x−9=0
x=9
interesują nas mniejsze do zera, więc:
x∊(0;9)
26 kwi 18:36
martuniaaa xD: zad 11
jest to ciag arytmetyczny
a1 = −4
a2 = 2
a3 = 5
wec r= 3
26 kwi 18:41
martuniaaa xD: a1 = −1 sorka
26 kwi 18:42
martuniaaa xD: zad 9
wychodzi mi ze 4/5 ale nie jestem pewna co do tego
26 kwi 18:47
Kejt:
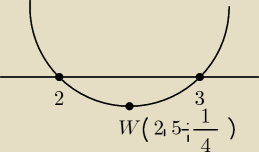
1a)
y=x
2−5x+6
Δ=1
| | −b | | −(−5) | | 5 | |
p= |
| = |
| = |
| =2,5 |
| | 2a | | 2 | | 2 | |
x
1=2
x
2=3
| | 1 | |
postać kanoniczna: f(x)=a(x−p)2+q czyli: f(x)=(x−2,5)2− |
| |
| | 4 | |
postać iloczynowa: f(x)=a(x−x
1)(x−x
2)=f(x)=(x−2)(x−3)
przy współrzędnych wierzchołka jest:
26 kwi 19:07
Kejt: przy postaci iloczynowej jest: f(x)=a(x−x1)(x−x2) czyli: f(x)=(x−2)(x−3)
26 kwi 19:12
Mati:
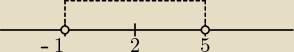
4.
|x−2| <3
x−2=0
x=2
26 kwi 19:22
Mati:
|x+3| ≤ 2
x+3=0
x=−3
26 kwi 19:24
Mati: |x+3|=5
x+3=5 lub x+3= −5
więc
x= 2 lub x = −8
26 kwi 19:26
Kejt: 2.
a) 2x
3−x
2+2x−1=0
x
2(2x−1)+1(2x−1)=0
(x
2+1)(2x−1)=0
x
2=1 v 2x−1=0
x
2=−1 v 2x=1
b) 5x
3+2x
2−5x−2=0
x
2(5x+2)−1(5x+2)=0
(x
2−1)(5x+2)=0
x
2−1=0 v 5x+2=0
(x+1)(x−1)=0 v 5x=−2
x=−1 v x=1
c) 5x
3=25x
5x
3−25x=0
5x(x
2−5)=0
5x(x+
√5)(x−
√5)=0
5x=0 v x+
√5=0 v x−
√5=0
x=0 v x=−
√5 v x=
√5
x∊{−
√5;0;
√5}
26 kwi 19:26
Kejt: biorę 6 i 7..
26 kwi 19:30
Mati: Napisz równanie prostej prostopadłej i równoległej do y=3x+7 przechodzącej przez punkt
P=(−2;5)
równoległa:
y=3x+b
5=3*(−2) +b
5= −6+b
−6+b=5
b=11
y=3x+11
Prostopadła:
26 kwi 19:31
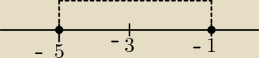
Bigosek: zad 4
a) |x−2|<3
x − 2 < 3 i x − 2 > −3
x < 5 x > −1
odp x ∊ ( −1 ; 5 )
b) |x+3| >= 2
x + 3 >= 2 lub x + 3 <= −2
x >= −1 x <= −5
odp x ∊ (−∞; −5> ∪ <−1; +∞)
c) |x+3|=5
x + 3 = 5 lub x + 3 = −5
x = 2 x = −8
odp x ∊ {−8; 2}
26 kwi 19:39
Mati: 9)Obl m jeśli punkt P(−3;8) należy do wykresu funkcji f(x)=(3m−2)x+4m−2
Dla jakiego m funkcja jest rosnąca?
8 = (3m−2)−3 +4m−2
8 = −9m +6 +4m −2
−9m +6 +4m −2 =8
−5m = 8−6+2
−5m = 4
rosnąca jest dla:
3m−2>0
3m>2
26 kwi 19:46
Mati: 11) Sprawdź czy ciąg an=3n−4 jest
a) arytmetyczny
b) geometryczny
a) an+1 = 3(n+1)−4 = 3n+3 −4 = 3n −1
an+1 − an
3n+3 −4 − 3n−1 = −2
26 kwi 19:52
Mati: Cześć Kasiu

26 kwi 19:53
Kejt: 7.
8=2(x+1)
2x+2=8
2x=6
x=3
x
2=−2(x+3)
x
2=−2x−6
x
2+2x+6=0
Δ=4−4*6=−20
Δ<0 => x∊∅
jeżeli się nie walnęłam..
26 kwi 19:54
Bigosek: 11) Sprawdź czy ciąg an=3n−4
jest
a) arytmetyczny
b) geometryczny
an= 3n − 4
an+1 = 3(n+1) −4
an+1 = 3n − 1
an+1 − an = 3n − 1 − (3n − 4) = 3n − 1 − 3n + 4 = 3
jest to ciąg arytmetyczny
26 kwi 19:54
Kejt: cześć Mati

26 kwi 19:54
Kejt: w 6 nie ma żadnej literówki?
26 kwi 19:55
ICSP: Kejt 6 zrób


26 kwi 19:56
Kejt:
6.
f(x)=ax+b
f(−3)=4
f(−3)=−3a+b
−3a+b=4
a z tym f(z) to chyba coś nie tak jest, hm?
26 kwi 20:01
Mati: A to 8? Bo mi coś ujemnego wychodzi..
26 kwi 20:16
Kejt: brak zainteresowania autora..
26 kwi 20:23
Rollnick: Cały czas się tym interesuję

Zadania 1, 2, 4, 7 miałem identycznie zrobione

w 9 i 11 błędy były ale już wiem jakie

26 kwi 20:40
Kejt: taak tylko, ze są pytania z naszej strony..a tu zero odzewu..nie pomyliłeś się w przepisywaniu?
26 kwi 20:42
Rollnick: Niee.. przepisuję zadania z kartki którą dostałem od babki z matmy..
26 kwi 20:43
Kejt: no to 6. jest jak dla mnie nie do rozwiązania..
26 kwi 20:45
Rollnick: f(−3)=4
f(z)=−5 lub f(2)=−5
bo to są zadanie pisane ręcznie przez nią.. i to Z może być dwójką jak się dokładnie temu
przyjrzeć..
26 kwi 20:49
Kejt: pewnie, że tam 2 jest..daj chwilkę, już piszę.
26 kwi 20:53
Kejt:
6.
f(x)=ax+b
f(−3)=4
f(−3)=−3a+b
−3a+b=4
f(2)=−5
f(2)=2a+b
2a+b=−5
−3a+b=4
2a+b=−5
rozwiąż ten układ.. mi się już nie chce

26 kwi 20:55
ICSP: widzę że ustalanie równania prostej układem równań

.
26 kwi 20:57
Kejt: a co.. coś nie tak?
26 kwi 20:58
ICSP: nic

Po prostu nie lubię metod do okola świata.
26 kwi 20:59
Kejt: mnie tak uczyli.. jak znasz prostszą metodę to z chęcią ją poznam..
26 kwi 21:00
Rollnick: Ja również

26 kwi 21:01
Kejt: może ze wzoru..? prostej przechodzącej przez dwa punkty..
26 kwi 21:02
ICSP: mamy dwa punkty:
A(1;4)
B(−3;−4)
prosta ma równanie: y = ax + b
liczymy jej współczynnik kierunkowy:
| | −4−4 | | −8 | |
a = |
| = |
| = 2 |
| | −3−1 | | −4 | |
teraz podczas pisania wzoru funkcji w pamięci liczymy współczynnik b.
y = 2x + 2
26 kwi 21:04
ICSP: Oczywiście to nie jest twoja prosta. Te dwa punkty wymyśliłem na poczekaniu.
26 kwi 21:04
Rollnick: Dzięki wszystkim za pomoc

mam nadzieję ze jakoś to bedzie

26 kwi 21:14
Alicja: (x+1)+2(x+1)=6 dla X<−1
11 cze 18:53
Alicja: (81x2−16)*(27x3+8)=0
11 cze 18:56
 wiec proszę was o pomoc w rozwiązaniu tych zadań.
wiec proszę was o pomoc w rozwiązaniu tych zadań.  Z góry serdecznie dziękuję
Z góry serdecznie dziękuję  1) Rozwiąż nierówność (muszą być wykresy)
a) x2−5x+6>0
b) x2<9x
1a) narysuj wykres funkcji y=x2−5x+6 (x1,x2,w) Podaj postać kanoniczną i iloczynową
2)Rozwiąż równania
a) 2x3−x2+2x−1=0
b) 5x3+2x2−5x−2=0
c) 5x3=25x
3)Znajdź Ymin, Ymax w przedziale <−1;2> jeśli y=x2−x
4)Rozwiąż nierówność i równanie
a) |x−2|<3
b) |x+3|>/2 −> nie wiem jak się tu robi znak mniejsze bądź równe
1) Rozwiąż nierówność (muszą być wykresy)
a) x2−5x+6>0
b) x2<9x
1a) narysuj wykres funkcji y=x2−5x+6 (x1,x2,w) Podaj postać kanoniczną i iloczynową
2)Rozwiąż równania
a) 2x3−x2+2x−1=0
b) 5x3+2x2−5x−2=0
c) 5x3=25x
3)Znajdź Ymin, Ymax w przedziale <−1;2> jeśli y=x2−x
4)Rozwiąż nierówność i równanie
a) |x−2|<3
b) |x+3|>/2 −> nie wiem jak się tu robi znak mniejsze bądź równe  c) |x+3|=5
5) Napisz równanie prostej prostopadłej i równoległej do y=3x+7 przechodzącej przez punkt
P=(−2;5)
6) Wyznacz równanie prostej jeśli f(−3)=4 i f(z)=−5
7) Rozwiąż równanie
c) |x+3|=5
5) Napisz równanie prostej prostopadłej i równoległej do y=3x+7 przechodzącej przez punkt
P=(−2;5)
6) Wyznacz równanie prostej jeśli f(−3)=4 i f(z)=−5
7) Rozwiąż równanie
 a) x2−5x+6>0
Δ=25−6*4=25−24=1
√Δ=1
a) x2−5x+6>0
Δ=25−6*4=25−24=1
√Δ=1
 b) x2<9x
x2−9x<0
x(x−9)<0
x=0 v x−9=0
x=9
interesują nas mniejsze do zera, więc:
x∊(0;9)
b) x2<9x
x2−9x<0
x(x−9)<0
x=0 v x−9=0
x=9
interesują nas mniejsze do zera, więc:
x∊(0;9)
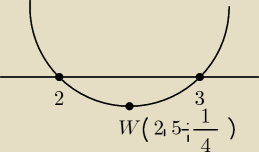 1a)
y=x2−5x+6
Δ=1
1a)
y=x2−5x+6
Δ=1
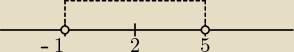 4.
|x−2| <3
x−2=0
x=2
4.
|x−2| <3
x−2=0
x=2
 |x+3| ≤ 2
x+3=0
x=−3
|x+3| ≤ 2
x+3=0
x=−3




 Zadania 1, 2, 4, 7 miałem identycznie zrobione
Zadania 1, 2, 4, 7 miałem identycznie zrobione  w 9 i 11 błędy były ale już wiem jakie
w 9 i 11 błędy były ale już wiem jakie 

 .
.
 Po prostu nie lubię metod do okola świata.
Po prostu nie lubię metod do okola świata.

 mam nadzieję ze jakoś to bedzie
mam nadzieję ze jakoś to bedzie 