Oblicz pole
Piotrek:
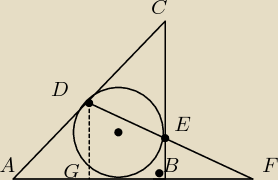
Okrąg wpisany w trójkąt prostokątny ABC o bokach długości AB|=8, |BC|=6, |AC|=10 jest styczny
do boków AC i BC w punktach D i E. Proste AB i DE przecinają się punkcie F. Oblicz pole
trójkąta EBF.
Mógłby ktoś pomóc?
Jakieś podobieństwo trójkątów DGF i EBF pewnie (bo EBF chyba nie jest podobny do ABC?
chociaż.... może być, ale nie wiem jak udowodnić).
26 kwi 17:25
Piotrek: Odświeżam
26 kwi 17:54
Piotrek: Ponownie
26 kwi 18:43
gosc: mi sie wydaje ze ABC daje do odczytania |DG|=3, |GB|=3
26 kwi 19:02
sowa:

witam
 2r
2r= a+b−c =>
r= 2
|AK|= |AD|=6, |DC|= |EC|=4 , |EB|= r= 2
|DG|=x , |AG|=y , |BF|= z
ΔAGD ~ ΔABC
| 6 | | y | |
| = |
| .... => y= 4,8
|
| 10 | | 8 | |
|GB|= 8− 4,8= 3,2
ΔGDF ~ ΔBEF
........ wykonaj obliczenia
z= |BF|= 4
| | |EB|*|BF| | |
P(ΔEBF)= |
| =..........
|
| | 2 | |
26 kwi 19:25
Piotrek: No ładnie

Dzięki

26 kwi 19:32
wolfy: heh sowa własnie rozkminiłem taki sam sposób i już chciałem zabrać się za rysowanie

tak apropo ten sposób na wyznaczenie poszczególnych odcinków figury przy pomocy kola wpisanego
działa tylko w trójkącie(tzn czy można np użyć go w trapezie prostokątnym?)
26 kwi 19:33
Piotrek: A skąd wiadomo, że SE jest równoległe do AB?
(S − środek okręgu)
26 kwi 19:34
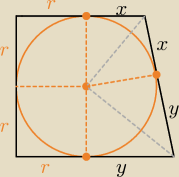
wolfy: tam na dole jest kwadrat o boku r?
26 kwi 19:35
Piotrek: No tak, na tym bazuje większość obliczeń
26 kwi 19:36
sowa:

26 kwi 19:37
wolfy: to właściwie było pytanie retoryczne

26 kwi 19:37
Piotrek: Dobra, to moje pytanie było głupie xD
26 kwi 19:38
ICSP: czy ty codziennie nicki zmieniasz?
26 kwi 19:38
wolfy: sowa zobacz 1 mój post w tym temacie i jak możesz rozwiej moje wątpliwości

26 kwi 19:38
ICSP: oczywiście do sowy mówię

26 kwi 19:38
sowa:
Właśnie nie uwidoczniłeś tego na Twoim rysunku

26 kwi 19:40
sowa:

.......... dla
ICSP
26 kwi 19:41
ICSP: 
dla *** lub jak wolisz
sowy
26 kwi 19:48
sowa:
26 kwi 19:49
 Okrąg wpisany w trójkąt prostokątny ABC o bokach długości AB|=8, |BC|=6, |AC|=10 jest styczny
do boków AC i BC w punktach D i E. Proste AB i DE przecinają się punkcie F. Oblicz pole
trójkąta EBF.
Mógłby ktoś pomóc?
Jakieś podobieństwo trójkątów DGF i EBF pewnie (bo EBF chyba nie jest podobny do ABC?
chociaż.... może być, ale nie wiem jak udowodnić).
Okrąg wpisany w trójkąt prostokątny ABC o bokach długości AB|=8, |BC|=6, |AC|=10 jest styczny
do boków AC i BC w punktach D i E. Proste AB i DE przecinają się punkcie F. Oblicz pole
trójkąta EBF.
Mógłby ktoś pomóc?
Jakieś podobieństwo trójkątów DGF i EBF pewnie (bo EBF chyba nie jest podobny do ABC?
chociaż.... może być, ale nie wiem jak udowodnić).
 witam
witam 2r= a+b−c => r= 2
|AK|= |AD|=6, |DC|= |EC|=4 , |EB|= r= 2
|DG|=x , |AG|=y , |BF|= z
ΔAGD ~ ΔABC
2r= a+b−c => r= 2
|AK|= |AD|=6, |DC|= |EC|=4 , |EB|= r= 2
|DG|=x , |AG|=y , |BF|= z
ΔAGD ~ ΔABC
 Dzięki
Dzięki 
 tak apropo ten sposób na wyznaczenie poszczególnych odcinków figury przy pomocy kola wpisanego
działa tylko w trójkącie(tzn czy można np użyć go w trapezie prostokątnym?)
tak apropo ten sposób na wyznaczenie poszczególnych odcinków figury przy pomocy kola wpisanego
działa tylko w trójkącie(tzn czy można np użyć go w trapezie prostokątnym?)





 .......... dla ICSP
.......... dla ICSP
 dla *** lub jak wolisz sowy
dla *** lub jak wolisz sowy
